题目内容
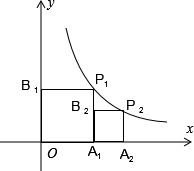 如图,正方形OA1P1B1和正方形A1A2P2B2的顶点P1,P2都在函数y=
如图,正方形OA1P1B1和正方形A1A2P2B2的顶点P1,P2都在函数y=| 4 |
| x |
(1)求点P1和点P2的坐标;
(2)求以P1为顶点且经过原点的抛物线的解析式;
(3)点P2是否在(2)中所求得的抛物线上?请说明理由.
考点:待定系数法求二次函数解析式,反比例函数图象上点的坐标特征,二次函数图象上点的坐标特征,正方形的性质
专题:计算题
分析:(1)设正方形OA1P1B1边长为a,P1(a,a),代入反比例解析式求出a的值确定出P1坐标,设正方形A1A2P2B2边长为b,P2(2+b,b),同理求出b的值,确定出P2坐标;
(2)根据题意设y=a(x-2)2+2,将(0,0)代入求出a的值,即可确定出解析式;
(3)将P2横坐标代入解析式求出y的值,与纵坐标比较即可.
(2)根据题意设y=a(x-2)2+2,将(0,0)代入求出a的值,即可确定出解析式;
(3)将P2横坐标代入解析式求出y的值,与纵坐标比较即可.
解答:解:(1)设正方形OA1P1B1边长为a,P1(a,a),
代入反比例解析式得:a2=4,
解得:a1=2,a2=-2(舍去),即P1(2,2),
设正方形A1A2P2B2边长为b,P2(2+b,b),
代入反比例解析式得:b(2+b)=4,
解得:b1=-1+
,b2=-1-
(舍去),即P2(1+
,-1+
);
(2)∵抛物线以P1为顶点,
∴y=a(x-2)2+2,
∵抛物线且经过原点,
∴0=4a+2,即a=-
,
∴y=-
x2+2x;
(3)将x=1+
代入得:y=
-1,
∴点P2在所求得的抛物线上.
代入反比例解析式得:a2=4,
解得:a1=2,a2=-2(舍去),即P1(2,2),
设正方形A1A2P2B2边长为b,P2(2+b,b),
代入反比例解析式得:b(2+b)=4,
解得:b1=-1+
| 5 |
| 5 |
| 5 |
| 5 |
(2)∵抛物线以P1为顶点,
∴y=a(x-2)2+2,
∵抛物线且经过原点,
∴0=4a+2,即a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
(3)将x=1+
| 5 |
| 5 |
∴点P2在所求得的抛物线上.
点评:此题考查了待定系数法求二次函数解析式,反比例函数与二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列判断正确的是( )
| A、“打开电视机,正在播NBA篮球赛”是必然事件 | ||||
B、“掷一枚硬币正面朝上的概率是
| ||||
| C、一组数据2,3,4,5,5,6的众数和中位数都是5 | ||||
D、甲组数据的方差
|
下列等式中,错误的是( )
| A、3x3+6x3=9x3 |
| B、2x2-3x2=-1 |
| C、3x3•6x3=18x6 |
| D、2x3•x2=2x5 |
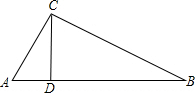 已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:
已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证: