题目内容
阅读与应用
计算:
+
+
+…+
解:因为:
=1-
,
=
-
,
=
-
,…
=
-
所以:
+
+
+…+
=(1-
)+(
-
)+(
-
)+…+(
-
)
=1-
+
-
+
-
+…+
-
=1-
阅读上述解题过程,请回答下列问题:
(1)
=
(1-
),
= ;…
= .
(2)计算
+
+
+…+
.
计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
解:因为:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9×10 |
| 1 |
| 9 |
| 1 |
| 10 |
所以:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 10 |
阅读上述解题过程,请回答下列问题:
(1)
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2007×2009 |
(2)计算
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 2007×2009 |
考点:有理数的混合运算
专题:规律型
分析:(1)根据题意得出一般性规律,计算即可得到结果;
(2)原式利用得出的规律变形,计算即可得到结果.
(2)原式利用得出的规律变形,计算即可得到结果.
解答:解:(1)
=
(
-
);
=
(
-
);
(2)原式=
(
-
+
-
+…+
-
)=
(
-
)=
.
故答案为:(1)
(
-
);
(
-
).
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2007×2009 |
| 1 |
| 2 |
| 1 |
| 2007 |
| 1 |
| 2009 |
(2)原式=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2007 |
| 1 |
| 2009 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2009 |
| 1003 |
| 6027 |
故答案为:(1)
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2007 |
| 1 |
| 2009 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列运算正确的是( )
| A、2x2y+3xy2=5x3y |
| B、(-x)3•(-x)2=-x5 |
| C、(-a3)2+(-a2)3=1 |
| D、2x3+x2=3x5 |
下列结论中正确是( )
| A、两个有理数的和一定大于其中任何一个加数 |
| B、零加上一个数仍得这个数 |
| C、两个有理数的差一定小于被减数 |
| D、零减去一个数仍得这个数 |
下列等式中,错误的是( )
| A、3x3+6x3=9x3 |
| B、2x2-3x2=-1 |
| C、3x3•6x3=18x6 |
| D、2x3•x2=2x5 |
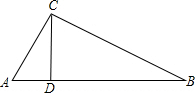 已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:
已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证: