题目内容
7.已知,点I是△ABC的内心,过点B作BP⊥BI交AI的延长线于点P(1)如图1,若BA=BC,
①求证:BP∥AC;
②设∠BAC=α(其中α为常数),求∠BCP;
(2)如图2,CM,BN为△ABC的角平分线,若BM+CN=6,∠BAC=60°,请你直接写出点P到直线BC的距离的最大值等于3$\sqrt{3}$.
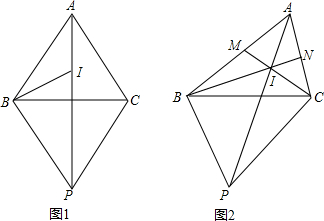
分析 (1)①由等腰三角形的性质证明∠BAC=∠BCA(设为α);由内切圆的性质求出∠ABI=90°-α,进而证明∠ABP+∠BAC=180°,即可解决问题;
②首先证明PB=BC,进而得到∠BCP=∠BPC;证明∠PBC=∠ACB=α,运用三角形的内角和定理,求出∠BCP,即可解决问题;
(2)根据△ABC为等边三角形时,P到直线BC的距离的最大求出最大值即可.
解答 解:(1)①如图,∵BA=BC,
∴∠BAC=∠BCA(设为α);
∵点I为△ABC的内心,
∴∠ABI=$\frac{180°-2α}{2}$=90°-α,
∴∠ABP=90°+90°-α=180°-α,
∴∠ABP+∠BAC=180°-α+α=180°,
∴BP∥AC.
②如图,∵BP∥AC,
∴∠CAP=∠APB,∠BCA=∠PBC,
∵AI是∠BAC的平分线,
∴∠BAP=∠CAP,
∴∠BAP=∠APB,
∴AB=PB;
∵AB=BC,
∴PB=BC,
∴∠BPC=∠BCP,
∴∠BCP=$\frac{180°-∠PBC}{2}$;
∵∠BCA=∠BAC=α,
∴∠PBC=∠BCA=∠BAC=α,
∴∠BCP=$\frac{180°-α}{2}$.
(2)当△ABC为等边三角形时,BC=BM+CN=6,
此时P到直线BC的距离的最大,
在等边三角形PBC中,BC=6,
P到直线BC的距离的最大值是3$\sqrt{3}$.
点评 该题主要考查了三角形内切圆的性质、三角形内角和定理、平行线的判定等几何知识点及其应用问题;牢固掌握三角形内切圆的性质等几何知识点是基础,灵活运用、解题是关键.

练习册系列答案
相关题目
12.已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
| A. | -7 | B. | 7 | C. | -5 | D. | 5 |
13.某商店在开业前,进了上衣、裤子与鞋子三种货物,其中裤子进了108条,三种货物进货数量的统计图如图甲所示.销售人员(销售上衣3人,销售裤子2人,销售鞋子1人)试销售了3天时间.经统计,这三天里三种货物每人每天销售数量统计图如图乙所示,三种货物3天的销售总量见表格(部分信息未给出).
(1)求所进上衣多少件?鞋子多少双?
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?
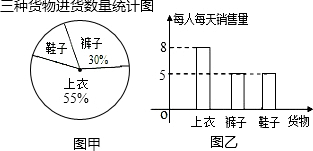
| 货物 | 上衣 (件) | 裤子 (条) | 鞋子 (双) |
| 3天的销售总量 | 72 | 30 | 15 |
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?

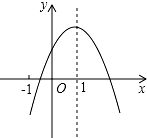 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
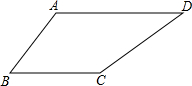 如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.