题目内容
19.已知x+y=-8,xy=8,求$y\sqrt{\frac{y}{x}}+x\sqrt{\frac{x}{y}}$的值.分析 根据x+y=-8,xy=8,可得x<0,y<0,把代数式根据二次根式的性质化简,再代入求值,即可解答.
解答 解:∵x+y=-8,xy=8,∴x<0,y<0,
∴$y\sqrt{\frac{y}{x}}+x\sqrt{\frac{x}{y}}$=$y\sqrt{\frac{xy}{x^2}}+x\sqrt{\frac{xy}{y^2}}=-\frac{y}{x}\sqrt{xy}-\frac{x}{y}\sqrt{xy}$=$({-\frac{y}{x}-\frac{x}{y}})\sqrt{xy}=-({\frac{{{y^2}+{x^2}}}{xy}})\sqrt{xy}$=$-\frac{{{{({x+y})}^2}-2xy}}{xy}\sqrt{xy}$,
原式=$-\frac{{{{({-8})}^2}-2×8}}{8}\sqrt{8}$=$-6\sqrt{8}=-12\sqrt{2}$.
点评 本题考查了二次根式的化简求值,解决本题的关键是根据二次根式的性质进行化简.

练习册系列答案
相关题目
4.下列调查中,适宜采用普查方式的是( )
| A. | 调查市场上酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| D. | 调查《最强大脑》节目的收视率情况 |
11.计算2x3•(-x2)的结果是( )
| A. | 2x | B. | -2x5 | C. | 2x6 | D. | x5 |
8.等腰三角形的两边长分别为3和6,那么该三角形的周长为( )
| A. | 12 | B. | 15 | C. | 10 | D. | 12或15 |
9.下列算式正确的是( )
| A. | a3+a2=a6 | B. | a3-a2=a6 | C. | a3•a2=a5 | D. | a3÷a2=a6 |
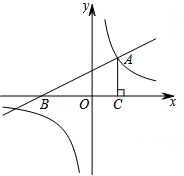 如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).
如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).