题目内容
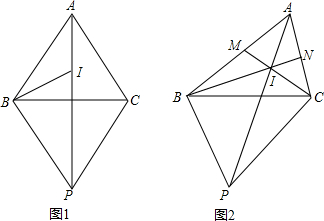
17.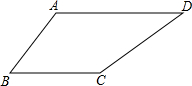 如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
分析 连接AC,根据题意求出∠BAC=60°,∠ACD=90°,利用含30°的直角三角形的性质即可求出AD的长.
解答 解:连接AC,如图: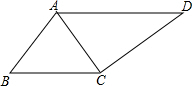
∵AB=BC=6cm,∠B=60°,
∴△ABC是等边三角形,
∴AC=6,∠BAC=∠ACB=60°,
∵∠A=120°,∠C=150°,
∴∠ACD=90°,∠CAD=30°,
∴AD=2AC=12.
点评 此题考查了含30°的直角三角形,熟练掌握含30°的直角三角形的性质是解本题的关键.

练习册系列答案
相关题目
8.等腰三角形的两边长分别为3和6,那么该三角形的周长为( )
| A. | 12 | B. | 15 | C. | 10 | D. | 12或15 |
5.根据如图给出的信息:若放入体积相同大球、体积相同小球各2个,水面将上升到( )
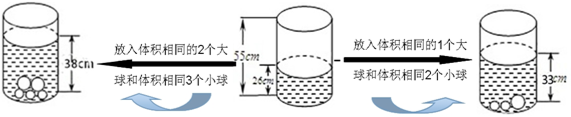

| A. | 35cm | B. | 36cm | C. | 37cm | D. | 39cm |
12.在?ABCD中,已知∠A-∠B=20°,则∠C=( )
| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
9.下列算式正确的是( )
| A. | a3+a2=a6 | B. | a3-a2=a6 | C. | a3•a2=a5 | D. | a3÷a2=a6 |
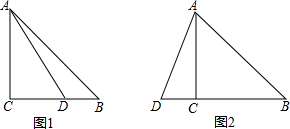 在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.
在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.