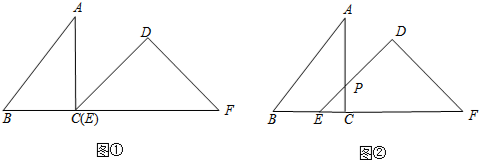Question

在Rt△ABC中，∠ACB=90°，tan∠BAC=

1

2

，点D在边AC上（不与A、C重合），连结BD，F为BD中点．

（1）若过点D作DE⊥AB于E，连结CF、EF、CE，如图1，当D为AC中点时，求tan∠DBE的值；
（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示，求证：BE-DE=2CF；
（3）若BC=3AD=6，将线段AD绕点A旋转，点F始终为BD的中点，则线段CF长度的最大值为

 

．

Answer 1

考点：几何变换综合题

专题：

分析：（1）利用锐角三角函数关系得出

DE

AE

=

BC

AC

=

1

2

，进而利用未知数表示出DE，AE，BE的长，进而得出答案；
（2）过点C作CE的垂线交BD于点G，设BD与AC的交点为Q．由tan∠BAC=

1

2

，得到

BC

AC

=

DE

AE

=

1

2

．证明△BCG∽△ACE，得到

BC

AC

=

GB

AE

=

1

2

．得到GB=DE，得到F是EG中点．于是CF=

1

2

EG，即可得到BE-DE=EG=2CF；
（3）分类讨论：当AD=

1

3

AC时，取AB的中点M，连接MF和CM，tan∠BAC=

1

2

，且BC=6，计算出AC=12，AB=6

5

．M为AB中点，则CM=3

5

，FM=

1

2

AD=2．当且仅当M、F、C三点共线且M在线段CF上时CF最大，此时CF=CM+FM=2+3

5

；当AD=

2

3

AC时，取AB的中点M，连接MF和CM，类似于情况1，可知CF的最大值为4+3

5

．即可得到线段CF长度的最大值．

解答：解：（1）设DE=x，
∵DE⊥AB，tan∠BAC=

1

2

，
∴

DE

AE

=

BC

AC

=

1

2

，
故AE=2x，则AD=

5

x，
∵D为AC中点，
∴AC=2

5

x，
则BC=

5

x，
由勾股定理得出：AB=5x，
则BE=3x，
故tan∠DBE的值为：

DE

BE

=

x

3x

=

1

3

；

（2）如图2，过点C作CE的垂线交BD于点G，设BD与AC的交点为Q．
由题意，tan∠BAC=

1

2

，
∴

BC

AC

=

DE

AE

=

1

2

．
∵D、E、B三点共线，
∴AE⊥DB．
∵∠BQC=∠AQD，∠ACB=90°，
∴∠QBC=∠EAQ．
∵∠ECA+∠ACG=90°，∠BCG+∠ACG=90°，
∴∠ECA=∠BCG．
∴△BCG∽△ACE．
∴

BC

AC

=

GB

AE

=

1

2

．
∴GB=DE．
∵F是BD中点，
∴F是EG中点．
在Rt△ECG中，CF=

1

2

EG，
∴BE-DE=EG=2CF；

（3）情况1：如图3，当AD=

1

3

AC时，取AB的中点M，连接MF和CM，
∵∠ACB=90°，tan∠BAC=

1

2

，且BC=6，
∴AC=12，AB=6

5

．
∵M为AB中点，
∴CM=3

5

，
∵AD=

1

3

AC，
∴AD=4
．∵M为AB中点，F为BD中点，
∴FM=

1

2

AD=2．
如图4：当且仅当M、F、C三点共线且M在线段CF上时CF最大，
此时CF=CM+FM=2+3

5

．
情况2：如图5，当AD=

2

3

AC时，取AB的中点M，连接MF和CM，
类似于情况1，可知CF的最大值为4+3

5

．
综合情况1与情况2，可知当点D在靠近点C的三等分点时，线段CF的长度取得最大值为：4+3

5

．
故答案为：4+3

5

．

点评：本题考查了三角形相似的判定与性质．也考查了旋转的性质和三角函数的定义以及直角三角形斜边上的中线等于斜边的一半．