题目内容
10.对于x2+kx-5=0,下列说法正确的是( )| A. | 方程有无实数根,要根据k的取值而定 | |
| B. | 无论k取何值,方程必有两个不相等的实数根 | |
| C. | 当k>0时,方程有两正根;当k<0时,方程有两负根 | |
| D. | 因为-5<0,因此方程两根肯定都为负数 |
分析 先根据一元二次方程的根的判别式确定出方程有实数根,再利用根与系数的关系来判断根的符号与b的关系.
解答 解:△=b2-4ac=k2-4×1×(-5)=k2+20,
∵k2≥0,
∴△>0,
∴原方程有两个不相等的实数根.B正确,A错误;
设方程的两根是x1、x2,那么
x1x2=-5,
又∵x1、x2不相等,
∴x1、x2必然异号.C、D错误.
故选:B.
点评 本题考查了根与系数的关系、根的判别式,解题的关键是知道一个方程有无实数根,只与根的判别式有关,要先判断方程有根,才能根据根与系数的关系确定根的情况.

练习册系列答案
相关题目
1.已知D、E分别是△ABC的边AB和AC的中点,F、G分别是AD、AE的中点,若△ABC的面积为16cm2,则四边形DEGF的面积为( )
| A. | 5cm2 | B. | 4cm2 | C. | 3cm2 | D. | 2cm2 |
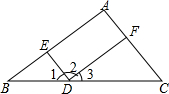 如图,推理填空:
如图,推理填空: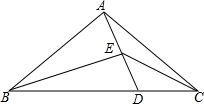 己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.
己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC. 如图,等腰Rt△ABC中,∠BAC=90°,已知A(0,2),C(5,0),求点B的坐标.
如图,等腰Rt△ABC中,∠BAC=90°,已知A(0,2),C(5,0),求点B的坐标. 在直角梯形ABCD中,AB∥DC,.AB⊥BC,AB=2CD,E为AB的中点,若△EBC沿EC折叠,使B点落在AD上的F点,连结EF、CE、CF.
在直角梯形ABCD中,AB∥DC,.AB⊥BC,AB=2CD,E为AB的中点,若△EBC沿EC折叠,使B点落在AD上的F点,连结EF、CE、CF.