题目内容
2. 如图,等腰Rt△ABC中,∠BAC=90°,已知A(0,2),C(5,0),求点B的坐标.
如图,等腰Rt△ABC中,∠BAC=90°,已知A(0,2),C(5,0),求点B的坐标.
分析 作BD⊥y轴,根据AAS可证明△ABD≌△COA,则BD=OA,AD=OC,即可求出点B的坐标.
解答 解:作BD⊥y轴,
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AB=AC,∠BAD+∠OAC=90°,
∵∠OCA+∠OAC=90°,
∴∠BAD=∠OCA,
在△ABD和△COA中,
$\left\{\begin{array}{l}{∠BDA=∠AOC=90°}\\{∠BAD=∠OCA}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△COA(AAS),
∴OA=BD,OC=AD,
∵A(0,2),C(5,0),
∴OA=2,OC=5,
∴BD=2,AD=5,
∴BD=2,OD=3,
∴B(-2,-3).
点评 本题主要考查了全等三角形的判定与性质以及点的坐标,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10.对于x2+kx-5=0,下列说法正确的是( )
| A. | 方程有无实数根,要根据k的取值而定 | |
| B. | 无论k取何值,方程必有两个不相等的实数根 | |
| C. | 当k>0时,方程有两正根;当k<0时,方程有两负根 | |
| D. | 因为-5<0,因此方程两根肯定都为负数 |
17.已知2是关于x的方程:x2-x+a=0的一个解,则2a-1的值是( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
 汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围.
汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围.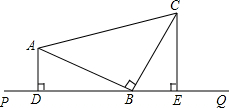 如图,△ABC中,AB=BC,∠ABC=90°,经过B点有一条直线PQ,分别过A、C作AD⊥PQ于D,CE⊥PQ于E.
如图,△ABC中,AB=BC,∠ABC=90°,经过B点有一条直线PQ,分别过A、C作AD⊥PQ于D,CE⊥PQ于E. 如图,在△ABC中,∠ACB=90°,在AC上取点D,使AD=BD,连结BD.若∠DBC=20°,求∠A的度数.
如图,在△ABC中,∠ACB=90°,在AC上取点D,使AD=BD,连结BD.若∠DBC=20°,求∠A的度数.