题目内容
1.已知D、E分别是△ABC的边AB和AC的中点,F、G分别是AD、AE的中点,若△ABC的面积为16cm2,则四边形DEGF的面积为( )| A. | 5cm2 | B. | 4cm2 | C. | 3cm2 | D. | 2cm2 |
分析 由D、E分别是△ABC的边AB和AC的中点,得到DE=$\frac{1}{2}$BC,DE∥BC,推出△ADE∽△ABC,得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{4}$,求得S△ADE=4cm2,由于F、G分别是AD、AE的中点,于是得到FG=$\frac{1}{2}$DE,GF∥DE,推出△AFG∽△ADE,得到$\frac{{S}_{△AFG}}{{S}_{△ADE}}$=$\frac{1}{4}$,求得S△AFG=1,于是得到结论.
解答 解:∵D、E分别是△ABC的边AB和AC的中点,
∴DE=$\frac{1}{2}$BC,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{4}$,
∴S△ADE=$\frac{1}{4}$S△ABC,
∵△ABC的面积为16cm2,
∴S△ADE=4cm2,
∵F、G分别是AD、AE的中点,
∴FG=$\frac{1}{2}$DE,GF∥DE,
∴△AFG∽△ADE,
∴$\frac{{S}_{△AFG}}{{S}_{△ADE}}$=$\frac{1}{4}$,
∴S△AFG=1,
∴四边形DEGF的面积=S△ADE-S△AFG=3cm2.
故选C.
点评 本题考查了相似三角形的判定和性质,三角形的中位线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.为了解决药品价格过高的问题,决定大幅度降低药品的价格,其中将原价a元的某种常用药降价40%,则降价后此药价格为( )
| A. | $\frac{a}{0.4}$元 | B. | $\frac{a}{0.6}$元 | C. | 60%a元 | D. | 40%a 元 |
10.对于x2+kx-5=0,下列说法正确的是( )
| A. | 方程有无实数根,要根据k的取值而定 | |
| B. | 无论k取何值,方程必有两个不相等的实数根 | |
| C. | 当k>0时,方程有两正根;当k<0时,方程有两负根 | |
| D. | 因为-5<0,因此方程两根肯定都为负数 |
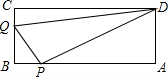 如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?
如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?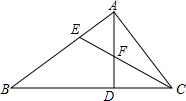 如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.
如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.