题目内容
20.某学校组织甲乙两班学生参加“美化校园”的义务劳动,如果甲班做2小时,乙班再做3小时,则恰好完成全部工作的一半;如果甲班做3小肘,乙班再做6小时,恰好完成全部工作的$\frac{7}{8}$,试问单独完成这项工作,甲乙两班各需多少时间.分析 单独完成这项工作甲需要x小时,乙需要y小时,则甲每小时完成全部工作的$\frac{1}{x}$,乙每小时完成全部工作的$\frac{1}{y}$,然后根据甲班做2小时,乙班再做3小时,则恰好完成全部工作的一半,甲班做3小肘,乙班再做6小时,恰好完成全部工作的$\frac{7}{8}$,即可列方程组求解.
解答 解:设单独完成这项工作甲需要x小时,乙需要y小时.
根据题意得:$\left\{\begin{array}{l}{\frac{2}{x}+\frac{3}{y}=\frac{1}{2}}\\{\frac{3}{x}+\frac{6}{y}=\frac{7}{8}}\end{array}\right.$,
设$\frac{1}{x}$=m,$\frac{1}{y}$=n,
则方程组可以化成$\left\{\begin{array}{l}{2m+3n=\frac{1}{2}}\\{3m+6n=\frac{7}{8}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{8}}\\{n=\frac{1}{12}}\end{array}\right.$,
则$\left\{\begin{array}{l}{x=8}\\{y=12}\end{array}\right.$.
答:单独完成这项工作甲需要8小时,乙需要12小时.
点评 本题考查了分式方程组的应用,根据方程组的特点化成二元一次方程组是关键.

练习册系列答案
相关题目
15.顺次连接四边形ABCD四条边的中点所得的四边形是菱形,则四边形ABCD一定是( )
| A. | 平行四边形 | B. | 矩形 | ||
| C. | 对角线相互垂直的四边形 | D. | 对角线相等的四边形 |
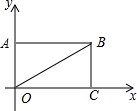 如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).
如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).