题目内容
13.(1)若A=x2-2xy+y2,B=x2+2xy+y2,则A+B=2x2+2y2;A-B=-4xy.(2)如果关于字母x的多项式-3x2+mx-5+nx2-x+3的值与字母x无关,则m=1,n=3.
分析 (1)把A与B代入A+B,A-B中,去括号合并即可得到结果;
(2)原式合并后,根据结果与x无关,求出m与n的值即可.
解答 解:(1)∵A=x2-2xy+y2,B=x2+2xy+y2,
∴A+B=x2-2xy+y2+x2+2xy+y2=2x2+2y2,A-B=x2-2xy+y2-x2-2xy-y2=-4xy;
(2)原式=(n-3)x2+(m-1)x-2,
由结果与x无关,得到n-3=0,m-1=0,
解得:m=1,n=3.
故答案为:(1)2x2+2y2;-4xy;(2)1;3
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
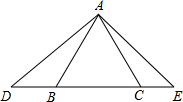 如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.
如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.