题目内容
3.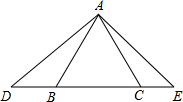 如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.
如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.(1)试写出图中所有的相似三角形;
(2)式子BC2=DB•CE成立吗?若成立,给出证明;若不成立,试说明理由.
分析 (1)根据相似三角形的判定及已知可得到题中存在的相似三角形;
(2)根据相似三角形的对应边成比例及已知,即可求得DB、BC、CE之间的关系.
解答 解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°.
∴∠D+∠DAB=60°,∠E+∠CAE=60°.
∵∠DAE=120°,
∴∠DAB+∠EAC=60°.
∴∠D=∠CAE,∠E=∠DAB.
∵∠D=∠D,∠E=∠E,
∴△DAE∽△DBA∽△ACE.
∴相似三角形共有3对.
(2)∵△DBA∽△ACE,
∴DB:AC=AB:CE.
∵AB=AC=BC,
∴BC2=DB•CE.
点评 此题考查了相似三角形的判定和性质:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.已知m2-n2=4,那么(m+n)2(m-n)2的结果是( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
 已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12.
已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12. 如图,边长为a、2的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=4cm时阴影部分的面积.
如图,边长为a、2的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=4cm时阴影部分的面积.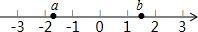 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.