Question

14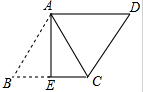．如图，在?ABCD中，AB=$\sqrt{13}$，AD=4，将?ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为（　　）

• A． $\sqrt{17}$
• B． $\sqrt{3}$
• C． $\frac{5}{2}$
• D． 3

Answer 1

分析 依据平行四边形的性质可得到BC=4，然后由翻折的性质可知BE=EC=2，∠BEA=∠AEC=90°，最后在Rt△ABE中，依据勾股定理求解即可．

解答 解：∵四边形ABCD为平行四边形，
∴BC=AD=4．
由翻折的性质可知：BE=EC=2，∠BEA=∠AEC=90°．
在Rt△ABE中，AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=3．
故选：D．

点评 本题主要考查的是翻折的性质、勾股定理的应用、平行四边形的性质，掌握相关知识是解题的关键．