题目内容
19.不等式组$\left\{\begin{array}{l}{3(x+2)>x-4}\\{-\frac{2}{3}x+4≥2}\end{array}\right.$的最大整数解是x=3.分析 根据解一元一次不等式组的方法可以求得原不等式组的解集,从而可以得到原不等式组的最大整数解.
解答 解:$\left\{\begin{array}{l}{3(x+2)>x-4}&{①}\\{-\frac{2}{3}x+4≥2}&{②}\end{array}\right.$,
由①,得x>-5,
由②,得x≤3,
故原不等式组的解集是-5<x≤3,
即不等式组$\left\{\begin{array}{l}{3(x+2)>x-4}\\{-\frac{2}{3}x+4≥2}\end{array}\right.$的最大整数解是x=3,
故答案为:x=3.
点评 本题考查一元一次不等式组的整数解,解题的关键是明确一元一次不等式组的解法.

练习册系列答案
相关题目
14.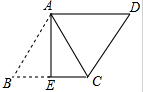 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )| A. | $\sqrt{17}$ | B. | $\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 3 |
3.下列函数中,其图象与x轴有两个交点的是( )
| A. | y=8(x+2015)2+2016 | B. | y=8(x-2015)2+2016 | ||
| C. | y=-8(x-2015)2-2016 | D. | y=-8(x+2015)2+2016 |
 如图,已知△ABC的面积为8cm2,BP为∠ABC的角平分线,AP垂直BP于点P,则△PBC的面积为4cm2.
如图,已知△ABC的面积为8cm2,BP为∠ABC的角平分线,AP垂直BP于点P,则△PBC的面积为4cm2.