题目内容
19．
如图，将含有45°角的三角板的两个顶点放在直尺的对边上，如果∠1=20°，那么∠2=25°．
分析 利用两直线平行，内错角相等作答．
解答 
解：根据题意可知，两直线平行，内错角相等，
∴∠1=∠3，
∵∠3+∠2=45°，
∴∠1+∠2=45°
∵∠1=20°，
∴∠2=25°．
故答案为25．
点评 本题主要考查了两直线平行，内错角相等的性质，需要注意隐含条件，直尺的对边平行，等腰直角三角板的锐角是45°的利用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．
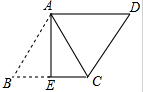如图，在?ABCD中，AB=$\sqrt{13}$，AD=4，将?ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为（ ）
如图，在?ABCD中，AB=$\sqrt{13}$，AD=4，将?ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为（ ）| A． | $\sqrt{17}$ | B． | $\sqrt{3}$ | C． | $\frac{5}{2}$ | D． | 3 |
7．下列三条线段能构成三角形的是（ ）
| A． | 1，2，3 | B． | 3，4，5 | C． | 7，10，18 | D． | 4，12，7 |
4．已知函数y=$\left\{\begin{array}{l}{2x+1}&{（x≥0）}\\{4x}&{（x＜0）}\end{array}\right.$，当x=2时，函数值y为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
11．若x2+mx+$\frac{1}{4}$是一个完全平方式，则m的值是（ ）
| A． | 1 | B． | ±1 | C． | $\frac{1}{2}$ | D． | ±$\frac{1}{2}$ |
9．下列给出的五组条件中，能判定△ABC与△DEF全等的概率是（ ）
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E，BC=EF；
③AB=DE，BC=EF，∠A=∠D；
④AC=DF，∠A=∠D，∠B=∠E；
⑤∠A=∠D，∠C=∠F，AC=EF．
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E，BC=EF；
③AB=DE，BC=EF，∠A=∠D；
④AC=DF，∠A=∠D，∠B=∠E；
⑤∠A=∠D，∠C=∠F，AC=EF．
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |