题目内容
9.点P(m,n)在二次函数y=x2-2x的图象上,当0≤m≤3时,则n的取值范围是-1≤n≤3.分析 将二次函数解析式整理成顶点式形式,然后确定出对称轴,再根据二次函数的增减性求出m取值范围内的最大值,然后写出n的取值范围即可.
解答 解:y=x2-2x=(x-1)2-1,
所以,对称轴为直线x=1,
∵0≤m≤3,a=1>0,
∴当m=1时,n有最小值-1,
当m=3时,n有最大值为32-2×3=9-6=3,
所以,n的取值范围是-1≤n≤3.
故答案为:-1≤n≤3.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性以及最值问题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.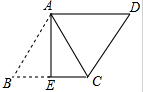 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )| A. | $\sqrt{17}$ | B. | $\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 3 |
13. 如图,直线a、b 被直线c所截,下列式子中能使直线a∥b( )
如图,直线a、b 被直线c所截,下列式子中能使直线a∥b( )
 如图,直线a、b 被直线c所截,下列式子中能使直线a∥b( )
如图,直线a、b 被直线c所截,下列式子中能使直线a∥b( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1=∠4 | D. | ∠1=∠5 |
 如图,小华把同心圆纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上),已知大圆半径为30cm,小圆半径为20cm,则飞镖击中阴影区域的概率是$\frac{5}{9}$.
如图,小华把同心圆纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上),已知大圆半径为30cm,小圆半径为20cm,则飞镖击中阴影区域的概率是$\frac{5}{9}$. △ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(-2,-2).
△ABC的边AC在正方形网格中的位置如图所示,已知每个小正方形的边长为1,顶点A坐标为(-2,-2).