题目内容
2.关于x的方程3kx2+12x+2=0有实数根,则k的取值范围是k≤6.分析 由于k的取值不确定,故应分k=0(此时方程化简为一元一次方程)和k≠0(此时方程为二元一次方程)两种情况进行解答.
解答 解:当k=0时,原方程可化为12x+2=0,解得x=-$\frac{1}{6}$;
当k≠0时,此方程是一元二次方程,
∵方程3kx2+12x+2=0有实数根,
∴△≥0,即△=122-4×3k×2≥0,解得k≤6.
∴k的取值范围是k≤6.
故答案为:k≤6.
点评 本题考查的是根的判别式,注意掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系,同时解答此题时要注意分k=0和k≠0两种情况进行讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.-4$\frac{2}{3}$的倒数是( )
| A. | 4$\frac{2}{3}$ | B. | -4$\frac{3}{2}$ | C. | -$\frac{14}{3}$ | D. | -$\frac{3}{14}$ |
14.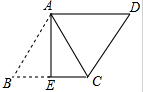 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
 如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在?ABCD中,AB=$\sqrt{13}$,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )| A. | $\sqrt{17}$ | B. | $\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 3 |
7.下列三条线段能构成三角形的是( )
| A. | 1,2,3 | B. | 3,4,5 | C. | 7,10,18 | D. | 4,12,7 |
 如图,小华把同心圆纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上),已知大圆半径为30cm,小圆半径为20cm,则飞镖击中阴影区域的概率是$\frac{5}{9}$.
如图,小华把同心圆纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上),已知大圆半径为30cm,小圆半径为20cm,则飞镖击中阴影区域的概率是$\frac{5}{9}$. 如图,已知△ABC的面积为8cm2,BP为∠ABC的角平分线,AP垂直BP于点P,则△PBC的面积为4cm2.
如图,已知△ABC的面积为8cm2,BP为∠ABC的角平分线,AP垂直BP于点P,则△PBC的面积为4cm2.