题目内容
13.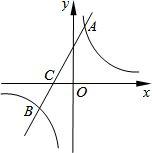 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)利用图象求不等式:$\frac{m}{x}$>kx+b.
分析 (1)利用正切函数求得A( 1,6),然后利用待定系数法即可求得.
(2)联立方程,解方程组即可求得B的坐标;
(3)根据函数的图象和交点坐标即可求得.
解答 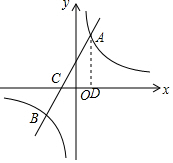 解:(1)过A作AD垂直x轴于点D,
解:(1)过A作AD垂直x轴于点D,
∵A的坐标为(n,6),
∴AD=6,
在Rt△ACD中,tan∠ACO=2,
∴$\frac{AD}{CD}=\frac{6}{2+n}=2$,
解得:n=1,
∴A的坐标为(1,6),
又∵A在$y=\frac{m}{x}$上,
∴m=6,
∵一次函数y=kx+b过A(1,6)和C(-2,0)
∴$\left\{\begin{array}{l}6=k+b\\ 0=-2k+b\end{array}\right.$
解得:$\left\{\begin{array}{l}k=2\\ b=4\end{array}\right.$
∴一次函数解析式为y=2x+4.
∴反比例函数解析式为:$y=\frac{6}{x}$,一次函数解析式为:y=2x+4.
(2)解方程组:$\left\{\begin{array}{l}y=\frac{6}{x}\\ y=2x+4\end{array}\right.$
解得:x1=1(舍去),x2=-3
∴B的坐标为(-3,-2).
(3)不等式$\frac{m}{x}>kx+b$的解集为:x<-3或0<x<1.
点评 此题考查了反比例函数与一次函数的交点问题.其知识点有解直角三角形,待定系数法求解析,解方程组等,此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
3.如果等腰三角形的两边长分别是方程x2-10x+21=0的两根,那么它的周长为( )
| A. | 17 | B. | 15 | C. | 13 | D. | 13或17 |
4.“黑洞”是恒星演化的最后阶段.根据有关理论,当一颗恒星衰老时,其中心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始坍缩,直到最后形成体积小、密度大的星体.如果这一星体的质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这种收缩使得它的半径达到施瓦氏(Schwarzschild)半径后,其引力就会变得相当强大,以至于光也不能逃脱出来,从而成为一个看不见的星体--黑洞.施瓦氏半径(单位:米)的计算公式是R=$\frac{2GM}{{c}^{2}}$,其中G=6.67×10-11牛•米2/千克2,为万有引力常数;M表示星球的质量(单位:千克);c=3×108米/秒,为光在真空中的速度.已知太阳的质量为2×1030千克,则可计算出太阳的施瓦氏半径为( )
| A. | 2.96×102米 | B. | 2.96×103米 | C. | 2.96×104米 | D. | 2.96×105米 |
1.在Rt△ABC中,∠C=90°,若$cosB=\frac{3}{5}$,则sinB的值得是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
18.如果两圆的半径长分别为3cm和5cm,圆心距为7cm,那么这两个圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 外离 | D. | 相交 |
7.根据昆明市旅游部门发布的统计数字显示,2014年中秋小长假,某景区三天共接待旅客约184000人,将184000用科学记数法表示应为( )
| A. | 1.84×104 | B. | 1.84×105 | C. | 18.4×103 | D. | 18.4×104 |
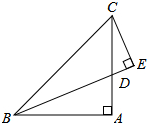 如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.
如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.