题目内容
6.如图,在正方形网格上有一个△ABC.(1)把△ABC沿水平方向向右平移4小方格得到△A′B′C′;
(2)在△ABC中作AB边上的高CD和BC边上的中线AE;
(3)若网格上的最小正方形边长为1,求△ABC的面积.
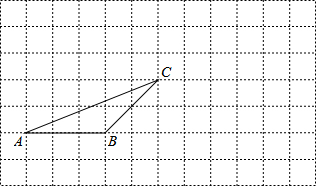
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用高线以及中线的定义分别得出即可;
(3)直接利用三角形面积求法得出即可.
解答  解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD,AE即为所求;
(3)S△ABC=$\frac{1}{2}$×2×3=3.
点评 此题主要考查了平移变换以及三角形的高线和中线的定义以及三角形面积求法,正确把握相关定义是解题关键.

练习册系列答案
相关题目
12. 如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
 如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )| A. | $5\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $\frac{48}{5}$ | D. | $\frac{24}{5}$ |
11.在实数范围内,二次根式$\sqrt{x-5}$有意义的x的取值范围是( )
| A. | x≤5 | B. | x>5 | C. | x<5 | D. | x≥5 |
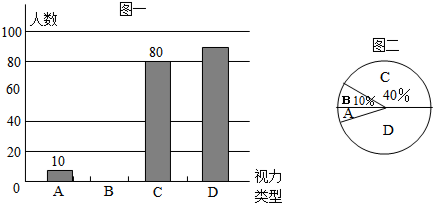
16.为了解本区初中学生的视力情况,教育局有关部门采用抽样调查的方法,从全区2万名中学生中抽查了部分学生的视力,分成如表四类进行统计
注:(4.3-4.5之间表示包括4.3及4.5)
根据图表完成下列问题:
(1)填完整表格及补充完整图一;
(2)“类型D”在扇形图(图二)中所占的圆心角是162度;
(3)本次调查数据的中位数落在C类型内;
(4)视力在5.0以下(不含5.0)均为不良,那么全区视力不良的初中学生估计11000人.
| 视力 | 类型 | 人数 |
| 视力在4.2及以下 | A | 10 |
| 视力在4.3-4.5之间 | B | 20 |
| 视力在4.6-4.9之间 | C | |
| 视力在5.0及以上 | D |
根据图表完成下列问题:
(1)填完整表格及补充完整图一;
(2)“类型D”在扇形图(图二)中所占的圆心角是162度;
(3)本次调查数据的中位数落在C类型内;
(4)视力在5.0以下(不含5.0)均为不良,那么全区视力不良的初中学生估计11000人.

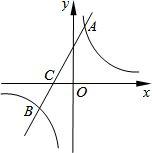 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.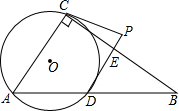 如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.
如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.


