题目内容
5.福建省第15届省运会将于2014年10月在漳州市举行,体训基地欲购买单价为100元的排球和单价为300元的篮球共100个.(1)如果购买两种球的总费用不超过24000元,并且篮球数不少于排球数的2倍,那么有哪几种购买方案?
(2)从节约开支的角度来看,你认为采用哪种方案最合算?
分析 (1)设购买排球x个,则购买篮球的个数是(100-x)个,根据购买两种球的总费用不超过24000元,并且篮球数不少于排球数的2倍,列出不等式组,解出x的值,即可得出答案;
(2)设购买篮球和排球的总费用为y元,则y=100x+300(100-x),即y=-200+30000,根据k=-200<0,所以y随x增大而减小,所以当x=33时,y最小,所以方案④最合算.
解答 解:(1)设购买排球x个,则购买篮球的个数是(100-x)个,
根据题意:$\left\{\begin{array}{l}{100-x≥2x}\\{100x+300(100-x)≤24000}\end{array}\right.$,
解得:30≤x≤$33\frac{1}{3}$,
∵x为整数,∴x取30,31,32,33,
∴有4种购买方案:
方案①:排球30个,篮球70个;
方案②:排球31个,篮球69个;
方案③:排球32个,篮球68个;
方案④:排球33个,篮球67个.
(2)设购买篮球和排球的总费用为y元,
则:y=100x+300(100-x),
即:y=-200+30000,
∵k=-200<0,
∴y随x增大而减小,
∴当x=33时,y最小,
∴方案④最合算.
点评 本题考查的是一元一次不等式组及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的不等关系.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
15.如图,是一个正六棱柱的主视图和左视图,则图中的a=( )


| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 1 |
16.5的绝对值是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | $\frac{1}{5}$ |
19.某种感冒病毒的直径为0.0000000031米,用科学记数法表示为( )
| A. | 3.1×10-10米 | B. | 3.1×10-9米 | C. | -3.1×109米 | D. | 0.31×10-8米 |
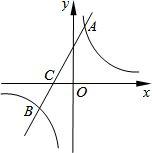 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.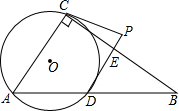 如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.
如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.


