题目内容
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
分析 根据题目中的不等式可以求得原不等式组的解集,由关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,可以求得t的取值范围,从而可以解答本题.
解答 解:$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}&{①}\\{\frac{x+3}{2}-t>x}&{②}\end{array}\right.$
解不等式①,得:x>5+$\frac{3}{2}$t,
解不等式②,得:x<3-2t,
∴不等式组的解集为5+$\frac{3}{2}$t<x<3-2t,
∵关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,
∴$\left\{\begin{array}{l}{(3-2t)-(5+\frac{3}{2}t)>2}\\{(3-2t)-(5+\frac{3}{2}t)≤4}\end{array}\right.$,
解得,$-\frac{12}{7}≤t<-\frac{8}{7}$,
故选A.
点评 本题考查一元一次不等式组的整数解,解答本题的关键是明确解一元一次不等式的方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.下列运算正确的是( )
| A. | -a(a-b)=-a2-ab | B. | (2ab)2÷a2b=4ab | C. | 2ab×3a=6a2b | D. | (a-1)(1-a)=a2 |
12.列方程解应用题:为了保护环境,节约用水,深圳按照《关于调整市水务(集团)有限公司自来水价格的通知》(深发改{2011}459 号)规定对供水范围内的居民用水实行三级阶梯水价收费如下表:
(1)若小明家去年1月份用水量20立方米,他家应缴费46元.
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
| 每户每月用水量 | 水费价格(单位:元/吨) |
| 不超过20 | 2.3 |
| 超过20吨且不超过30吨的部分 | a |
| 超过30吨的部分 | 4.6 |
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
17.下列图形中,是中心对称但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
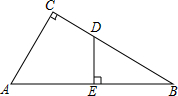 如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
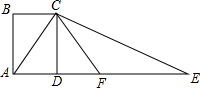 如图,四边形ABCD是长方形,AC⊥CE,F是AE的中点,CF=4.设AB=x,AD=y,则$\root{4}{{x}^{2}+(y-4)^{2}}$的值为2.
如图,四边形ABCD是长方形,AC⊥CE,F是AE的中点,CF=4.设AB=x,AD=y,则$\root{4}{{x}^{2}+(y-4)^{2}}$的值为2.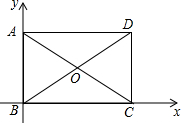 矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.
矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.