题目内容
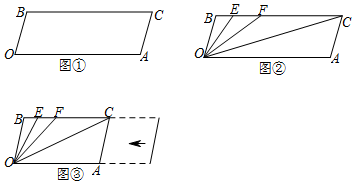
14.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以如图所示的方式“分裂”成2个,3个和4个连续奇数的和.若63也按照此规律进行“分裂”.则63分裂出的最大的那个奇数是41.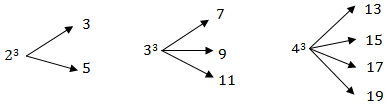
分析 观察不难发现,奇数的个数与底数相同,先求出到以6为底数的立方的最后一个奇数为止,所有的奇数的个数为20,再求出从3开始的第20个奇数即可得解.
解答 解:∵23有3、5共2个奇数,33有7、9、11共3个奇数,43有13、15、17、19共4个奇数,
…,
63共有6个奇数,
∴到63“分裂”出的奇数为止,一共有奇数:2+3+4+5+6=20,
又∵3是第一个奇数,
∴第20个奇数为20×1+1=41,
即63“分裂”出的奇数中,最大的奇数是41.
故答案为:41.
点评 本题考查了数字变换规律,有理数的乘方,观察数据特点,判断出底数是相应的奇数的个数是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
8.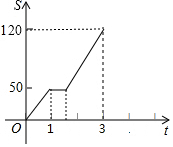 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |