题目内容
13.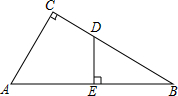 如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
分析 由垂直的定义得到∠DEB=90°,根据相似三角形的性质即可得到结论.
解答 解:∵DE⊥AB,
∴∠DEB=90°,
∴∠C=∠DEB,
∵∠B=∠B,
∴△BED∽△BCA,
∴$\frac{DE}{AC}=\frac{BD}{AB}$,
即$\frac{DE}{6}$=$\frac{5}{10}$,
∴DE=3,
故答案为:3.
点评 本题考查了相似三角形的判定和性质,垂直的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
1.已知一次函数y=ax+b,其中x和y的部分对应值如下表:
那么方程ax+b=0的解是x=1.5.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 7 | 5 | 3 | 1 | -1 | -3 |
8.已知点P到x轴距离为3,到y轴的距离为2,则P点坐标可以为( )
| A. | (3,2) | B. | (2,3) | C. | (-3,-2) | D. | (3,-2) |
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
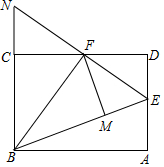 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线奇交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N,有下列四个结论: