题目内容
17.下列图形中,是中心对称但不是轴对称图形的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据轴对称图形与中心对称图形的概念求解.
解答 解:A、是轴对称图形,不是中心对称图形,故此选项错误;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项正确;
D、是轴对称图形,是中心对称图形,故此选项错误.
故选C.
点评 此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.

练习册系列答案
相关题目
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
8.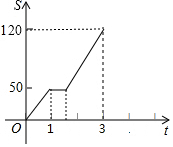 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |
12.对于问题:证明不等式a2+b2≥2ab,甲、乙两名同学的作业如下:
甲:根据一个数的平方是非负数可知(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
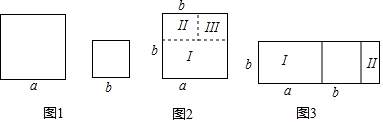
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )
甲:根据一个数的平方是非负数可知(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab.
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )

| A. | 甲、乙都对 | B. | 甲对,乙不对 | C. | 甲不对,乙对 | D. | 甲、乙都不对 |
2. 如图,∠1的同旁内角共有( )
如图,∠1的同旁内角共有( )
 如图,∠1的同旁内角共有( )
如图,∠1的同旁内角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.如果函数y=ax2+2x+1的图象不经过第四象限,那么实数a的取值范围为( )
| A. | a<0 | B. | a=0 | C. | a>0 | D. | a≥0 |
7.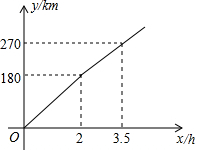 某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
 某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
某汽车从A开往360km外的B,全程的前一部分为高速公路,后一部分为普通公路.若汽车在高速公路和普通公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )| A. | 汽车在高速公路上的行驶速度为100km/h | |
| B. | 普通公路总长为90km | |
| C. | 汽车在普通公路上的行驶速度为60km/h | |
| D. | 汽车出发后4h到B地 |
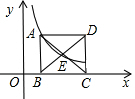 已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).