题目内容
19.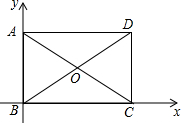 矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.
矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.(1)以点B为原点建立如图所示的平面直角坐标系,则点D的坐标为(4$\sqrt{3}$,4);
(2)过点O的直线EF交线段AD,BC分别于点E,F,若∠EOD为直角三角形,求点E的坐标.
分析 (1)易知AB=CD=OA=OB=OC=OD=4,在Rt△BCD中求出BC即可;
(2)分两种情形求解①如图2中,当EF⊥AD时,易知AE=DE=4,此时E(4,4).②如图3中,当EF⊥BD时,分别求解即可;
解答 解:(1)如图1中,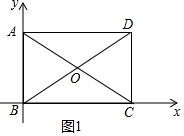
∵四边形ABCD是矩形,
∴OA=OC=OD=OB,
∴△ABO是等边三角形,
∴AB=CD=OD=OC=4,
∴BD=8,
在Rt△BCD中,BC=$\sqrt{B{D}^{2}-D{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴D(4$\sqrt{3}$,4),
故答案为(4$\sqrt{3}$,4).
(2)①如图2中,当EF⊥AD时,易知AE=DE=4,此时E(4,4).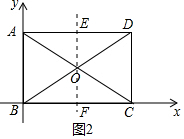
②如图3中,当EF⊥BD时,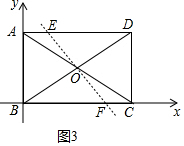
在Rt△EOD中,cos∠EDO=$\frac{OD}{DE}$=$\frac{AD}{BD}$,
∴$\frac{4}{DE}$=$\frac{4\sqrt{3}}{8}$,
∴DE=$\frac{8\sqrt{3}}{3}$,
∴AE=8-$\frac{8\sqrt{3}}{3}$,
∴E(8-$\frac{8\sqrt{3}}{3}$,4),
综上所述,满足条件的点E坐标为(4,4)或(8-$\frac{8\sqrt{3}}{3}$,4).
点评 本题考查坐标与图形的性质、矩形的性质,直角三角形的判定,锐角三角函数等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
8.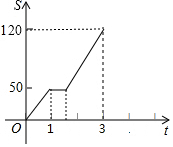 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |

 如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).
如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).