题目内容
2.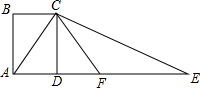 如图,四边形ABCD是长方形,AC⊥CE,F是AE的中点,CF=4.设AB=x,AD=y,则$\root{4}{{x}^{2}+(y-4)^{2}}$的值为2.
如图,四边形ABCD是长方形,AC⊥CE,F是AE的中点,CF=4.设AB=x,AD=y,则$\root{4}{{x}^{2}+(y-4)^{2}}$的值为2.
分析 由矩形的性质得出CD=AB=x,∠ADC=∠CDF=90°,由直角三角形斜边上的中线性质得出CF=$\frac{1}{2}$AE=AF=4,求出DF=4-y,在Rt△CDF中,由勾股定理得出得:CF=$\sqrt{{x}^{2}+(4-y)^{2}}$=4,即可得出答案.
解答 解:∵四边形ABCD是矩形,
∴CD=AB=x,∠ADC=90°,
∴∠CDF=90°,
∵AC⊥CE,F是AE的中点,
∴CF=$\frac{1}{2}$AE=AF=4,
∴DF=4-y,
在Rt△CDF中,由勾股定理得:CF=$\sqrt{{x}^{2}+(4-y)^{2}}$=4,
∴$\sqrt{{x}^{2}+(y-4)^{2}}$=4,
∴$\root{4}{{x}^{2}+(y-4)^{2}}$=$\sqrt{4}$=2;
故答案为:2.
点评 本题考查了矩形的性质、直角三角形斜边上的中线性质、勾股定理、分数指数幂等知识;熟练掌握直角三角形的性质和勾股定理是解决问题的关键.

练习册系列答案
相关题目
8.已知点P到x轴距离为3,到y轴的距离为2,则P点坐标可以为( )
| A. | (3,2) | B. | (2,3) | C. | (-3,-2) | D. | (3,-2) |
13.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )
| A. | $\frac{720}{48+x}$-$\frac{720}{x}$=5 | B. | $\frac{720}{48}$+5=$\frac{720}{48+x}$ | C. | $\frac{720}{48}$-$\frac{720}{x}$=5 | D. | $\frac{720}{48}$-$\frac{720}{48+x}$=5 |
7.已知关于x的不等式组$\left\{\begin{array}{l}{\frac{2x+5}{3}-t>5}\\{\frac{x+3}{2}-t>x}\end{array}\right.$ 恰有三个整数根,则t的取值范围是( )
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
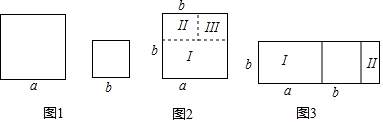
 如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).
如图中的四边形均为矩形,根据图形,利用图中的字母,写出一个正确的等式:(m+n)(a+b)=ma+mb+na+nb(答案不唯一).