��Ŀ����
4������ֱ�DZ�Ϊ6��ȫ�ȵĵ���Rt��AOB��Rt��CED�У���ͼ1��ʾ��λ�÷��ã�A��C�غϣ�O��E�غϣ���1����ͼ1��A��B��D����������꣮
��2��Rt��AOB�̶�������Rt��CED��x����ÿ��2����λ���ȵ��ٶ������˶�������D�˶�����B���غ�ʱֹͣ�����˶�x���Rt��AOB��Rt��CED���ص��������Ϊy����y��x֮��ĺ�����ϵʽ��
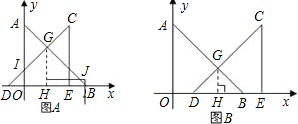
��3����Rt��CED�ԣ�2���е��ٶȺͷ����˶����˶�ʱ��x=4��ʱ��Rt��CED�˶�����ͼ2��ʾ��λ�ã���A��G��C����������ߵĽ���ʽ��
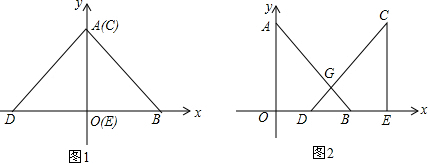
���� ��1��Rt��AOB��Rt��CED��ֱ�DZ�Ϊ6��������A��0��6����B��6��0����D��-6��0����
��2��Rt��CED��x����ÿ��2����λ�����ٶ������˶�����DE=6���������˶��������������������D����ͣ����y������D��y���Ҳ࣬���������ۣ��ڵ�һ������У��غϲ���Ϊ����ȫ�ȵ�ֱ�����Σ��ڵڶ�������У��غϲ���Ϊһ������ֱ�������Σ�����������
��3�����˶�ʱ��Ϊ4��ʱ����Ϊ��2���еڶ����������ʱA��G��C�����������������ô���ϵ����������⣮
���  �⣺��1����Ϊ����ֱ�DZ�Ϊ6��ȫ�ȵĵ���Rt��AOB��Rt��CED�У�
�⣺��1����Ϊ����ֱ�DZ�Ϊ6��ȫ�ȵĵ���Rt��AOB��Rt��CED�У�
�ɵã�A��0��6����B��6��0����D��-6��0����
��2����0��x��3ʱ��λ����ͼA��ʾ��
��GH��DB������ΪH����֪��OE=2x��EH=x��
DO=6-2x��DH=6-x��
��y=2S����IOHG=2��S��GHD-S��IOD��
=2[$\frac{1}{2}$��6-x��2-$\frac{1}{2}$��6-2x��2]
=2��$\frac{3}{2}$x2+6x��
=-3x2+12x
��3��x��6ʱ��λ����ͼB��ʾ��
��֪��DB=12-2x
��y=S��DGB=$\frac{1}{2}��\frac{\sqrt{2}}{2}DB��^{2}$=$\frac{1}{2}[\frac{\sqrt{2}}{2}$��12-2x��]2=x2-12x+36
��y��x�ĺ�����ϵʽΪ��$y=\left\{\begin{array}{l}{-3{x}^{2}+12x��0��x��3��}\\{{x}^{2}-12x+36��3��x��6��}\end{array}\right.$��
��3��ͼB�У���GH��OE������ΪH��
��x=4ʱ��OE=2x=8��DB=12-2x=4��
��GH=DH=$\frac{1}{2}$DB=2��OH=6-HB=6-$\frac{1}{2}$��DB=6-2=4
���֪A��0��6����G��4��2����C��8��6����
�ྭ��A��G��C����������ߵĽ���ʽΪ��y=$\frac{1}{4}$��x-4��2+2=$\frac{{x}^{2}}{4}$-2x+6��
���� ���⿼�鼸�α任���⣬�ؼ��ǰ��˶�����Ͷ��κ���������ϵ����������Ҫȫ�森

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -2��-$\frac{1}{2}$ | B�� | 0.1��1 | C�� | -2��$\frac{1}{2}$ | D�� | -43��43 |

| A�� | 3��2 | B�� | $\sqrt{2}$��1 | C�� | 4��3 | D�� | 2��$\sqrt{3}$ |
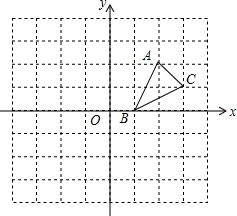 ��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0��
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0�� ��ͼ��ʾ����D�ǵȱ�������ABC��һ�㣬��CDΪһ������CD�·����ȱ�������CDE������AD��BE����֤����ACD�ա�BCE��
��ͼ��ʾ����D�ǵȱ�������ABC��һ�㣬��CDΪһ������CD�·����ȱ�������CDE������AD��BE����֤����ACD�ա�BCE��