题目内容
14.化简:$\sqrt{4\sqrt{3+2\sqrt{2}}+5}$=2$\sqrt{2}$+1.分析 根据完全平方公式把3+2$\sqrt{2}$化为($\sqrt{2}$+1)2的形式,根据$\sqrt{{a}^{2}}$=|a|进行化简,运用类似方法化简即可.
解答 解:原式=$\sqrt{4\sqrt{(\sqrt{2}+1)^{2}}+5}$
=$\sqrt{4\sqrt{2}+9}$
=$\sqrt{(2\sqrt{2}+1)^{2}}$
=2$\sqrt{2}$+1,
故答案为:2$\sqrt{2}$+1.
点评 本题考查的是二次根式的性质和化简,掌握$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
相关题目
9.若a(a-2b)+b2+2(a-b)+1=0,则a-b的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
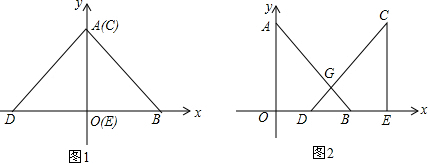
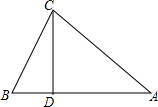 已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm
已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm