题目内容
13. 如图所示,点D是等边三角形ABC内一点,以CD为一边且在CD下方作等边三角形CDE,连接AD,BE,求证:△ACD≌△BCE.
如图所示,点D是等边三角形ABC内一点,以CD为一边且在CD下方作等边三角形CDE,连接AD,BE,求证:△ACD≌△BCE.
分析 根据等式的性质得出∠ACD=∠BCE,再利用SAS证明△ACD≌△BCE.
解答 证明:∵等边三角形ABC和等边三角形CDE,
∴∠ACB=∠DCE=60°,AC=BC,DC=CE,
∴∠ACB-∠BCD=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE.
点评 此题考查全等三角形的判定,关键是根据等式的性质得出∠ACD=∠BCE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
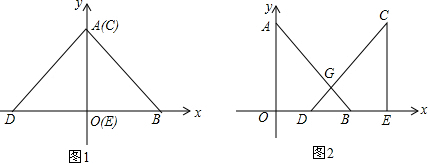
 从正面和上面看一个几何体的平面图形,如图所示.若这个几何体最多由n个小正方体组成,最少由m个小正方体组成,则m+n=16.
从正面和上面看一个几何体的平面图形,如图所示.若这个几何体最多由n个小正方体组成,最少由m个小正方体组成,则m+n=16.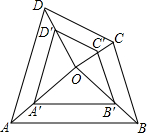 如图,点O是四边形ABCD与A′B′C′D′的位似中心,则$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{D′C′}{DC}$=$\frac{A′D′}{AD}$;∠ABC=∠A′B′C′,∠OCB=∠OC′B′.
如图,点O是四边形ABCD与A′B′C′D′的位似中心,则$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{D′C′}{DC}$=$\frac{A′D′}{AD}$;∠ABC=∠A′B′C′,∠OCB=∠OC′B′.