题目内容
12．分解因式：1-x2-2xy-y2=（1+x+y）（1-x-y）．分析 先分组，再根据完全平方公式分解因式，最后根据平方差公式分解因式即可．
解答 解：1-x2-2xy-y2
=1-（x2+2xy+y2）
=1-（x+y）2
=[1+（x+y）][（1-（x+y）]
=（1+x+y）（1-x-y），
故答案为：（1+x+y）（1-x-y）．
点评 本题考查了因式分解的应用，能正确分组是解此题的关键，注意：因式分解的方法有：提取公因式法、公式法、因式分解法、分组分解法．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
7．若|-2x|=3，则x的值是（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$或1 | C． | 1 | D． | -$\frac{3}{2}$或$\frac{3}{2}$ |
如图，两个同心圆中，大圆的半径AB、AC分别交小圆于点D、E，连接DC、EB交于点F，△BDF与△CEF是否全等？为什么？
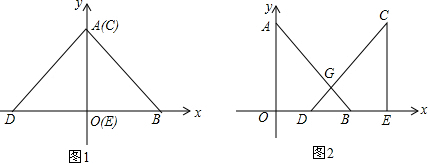
从正面和上面看一个几何体的平面图形，如图所示．若这个几何体最多由n个小正方体组成，最少由m个小正方体组成，则m+n=16．