题目内容
13.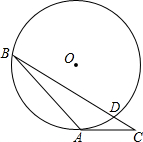 在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 2 |
分析 由于∠B=30°,则AD的长为定值,所以当DC与AC垂直时,CD最小,作直径AE,连结DE,过点D作DC′垂直切线于C′,交⊙O于B′,如图,先根据圆周角定理得到∠ADE=90°,∠E=∠B=30°,则∠EAD=60°,再在Rt△ADE中,利用含30度的直角三角形三边的关系得到AD=$\frac{1}{2}$AE=6,接着根据切线的性质得∠OAC=90°,则∠CAD=30°,然后在Rt△DAC′中计算出DC′=$\frac{1}{2}$AD=3,于是可判断CD的最小值为3.
解答 解: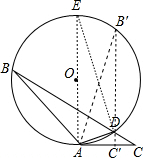 作直径AE,连结DE,过点D作DC′垂直切线于C′,交⊙O于B′,如图,
作直径AE,连结DE,过点D作DC′垂直切线于C′,交⊙O于B′,如图,
∵AE为直径,
∴∠ADE=90°,
∵∠E=∠B=30°,
∴∠EAD=60°,
在Rt△ADE中,AD=$\frac{1}{2}$AE=6,
∵AC是⊙O的切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠CAD=90°-60°=30°,
在Rt△DAC′中,∵∠DAC′=30°,
∴DC′=$\frac{1}{2}$AD=3,
∴当点C在C′点时,CD有最小值,最小值为3.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{2x+1≥0}\\{x-1<0}\end{array}\right.$的解集是( )
| A. | x≥-$\frac{1}{2}$ | B. | x<1 | C. | -$\frac{1}{2}$≤x<1 | D. | -$\frac{1}{2}$<x<1 |
8.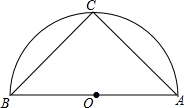 如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )
如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )
 如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )
如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )| A. | 3.5 | B. | 8 | C. | 12 | D. | 16 |
5.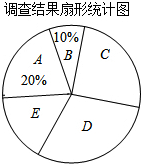 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
请根据图表中提供的信息解答下列问题:
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | 120 |
| B | 地面灰尘多,空气湿度低 | M |
| C | 汽车尾气排放 | N |
| D | 工厂造成的污染 | 180 |
| E | 其它 | 90 |
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
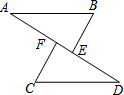 如图,AB∥CD,AB=CD,点E、F在AD上,且AE=DF.
如图,AB∥CD,AB=CD,点E、F在AD上,且AE=DF.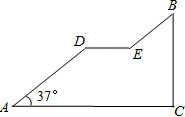 如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度. 已知函数y=-2x+6与函数y=3x-4.
已知函数y=-2x+6与函数y=3x-4.