题目内容
8.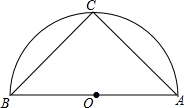 如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )
如图,在以AB为直径的半圆O中,点C是$\widehat{AB}$的中点,若AC=4,则△ABC的面积是( )| A. | 3.5 | B. | 8 | C. | 12 | D. | 16 |
分析 先根据圆周角定理,由AB为直径得到∠C=90°,由$\widehat{AC}$=$\widehat{BC}$得∠A=∠B,所以BC=AC=4,然后根据三角形面积公式求解.
解答 解:∵AB为直径,
∴∠C=90°,
∵点C是$\widehat{AB}$的中点,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠A=∠B,
∴BC=AC=4,
∴S△ABC=$\frac{1}{2}$×4×4=8.
故选B.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.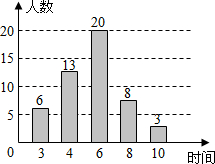 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
13.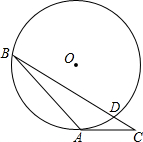 在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
 在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 2 |
17.下列计算正确的是( )
| A. | (2a)2=2a2 | B. | a6÷a3=a3 | C. | a3-a2=a6 | D. | 3a2+2a3=5a3 |
18.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+3y=10}\\{2x+z=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5m+n=-1}\\{4m+n=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2a+b=0}\\{ab=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3t+s=1}\\{\frac{1}{t}-s=11}\end{array}\right.$ |