题目内容
2．
已知函数y=-2x+6与函数y=3x-4．（1）在同一平面直角坐标系内，画出这两个函数的图象；
（2）求这两个函数图象的交点坐标．
分析 （1）利用描点法画出两函数图象；
（2）根据图象，直接写出两直线的交点坐标．
解答 
解：（1）如图；
（2）这两个函数图象的交点坐标为（2，2）．
点评 本题考查了两直线相交或平行问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解；若两条直线是平行的关系，那么它们的自变量系数相同，即k值相同．
练习册系列答案
相关题目
13．
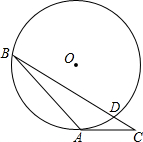在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是（ ）
在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是（ ）| A． | 1 | B． | 3 | C． | $\sqrt{3}$ | D． | 2 |
10．
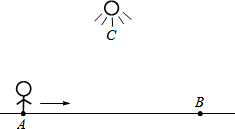我们常用“y随x的增大而增大（或减小）”来表示两个变量之间的变化关系．有这样一个情境：如图，小王从点A经过路灯C的正下方沿直线走到点B，他与路灯C的距离y随他与点A之间的距离x的变化而变化．下列函数中y与x之间的变化关系，最有可能与上述情境类似的是（ ）
我们常用“y随x的增大而增大（或减小）”来表示两个变量之间的变化关系．有这样一个情境：如图，小王从点A经过路灯C的正下方沿直线走到点B，他与路灯C的距离y随他与点A之间的距离x的变化而变化．下列函数中y与x之间的变化关系，最有可能与上述情境类似的是（ ）| A． | y=x? | B． | y=x+3 | C． | y=$\frac{3}{x}$? | D． | y=（x-3）2+3 |
17．下列计算正确的是（ ）
| A． | （2a）2=2a2 | B． | a6÷a3=a3 | C． | a3-a2=a6 | D． | 3a2+2a3=5a3 |
7．任意掷一枚质地均匀的骰子，掷出的点数大于4的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{6}$ |
11．
如图，直线a∥b，则∠ABD的度数是（ ）
如图，直线a∥b，则∠ABD的度数是（ ）| A． | 38° | B． | 48° | C． | 42° | D． | 100° |
12．分式$\frac{2}{x-3}$有意义，则x的取值范围是（ ）
| A． | x=3 | B． | x≠3 | C． | x≠-3 | D． | x=-3 |