题目内容
 如图,一次函数y1=x+1的图象与反比例函数y2=
如图,一次函数y1=x+1的图象与反比例函数y2=| k |
| x |
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y=
| k |
| x |
(3)根据图象说出当1≤x≤2时y2的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)直接把A(m,2)代入一次函数解析式y1=x+1求出m,从而得到A点坐标,然后把A点坐标代入反比例解析式可求出k,从而确定反比例函数解析式;
(2)观察第一象限两函数图象得到当0<x<1时,y1<y2;当x=1时,y1=y2;当x>1时,y1>y2;
(3)由于x=2时,y2=
,于是观察反比例函数图象得到当1≤x≤2时y2的取值范围为
≤y2≤1.
(2)观察第一象限两函数图象得到当0<x<1时,y1<y2;当x=1时,y1=y2;当x>1时,y1>y2;
(3)由于x=2时,y2=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)把A(m,2)代入y1=x+1得m+1=2,解得m=1,
所以A点坐标为(1,1),
把A(1,1)代入y2=
得k=1×1=1,
所以反比例函数解析式为y2=
;
(2)当0<x<1时,y1<y2;
当x=1时,y1=y2;
当x>1时,y1>y2;
(3)当1≤x≤2时y2的取值范围为
≤y2≤1.
所以A点坐标为(1,1),
把A(1,1)代入y2=
| k |
| x |
所以反比例函数解析式为y2=
| 1 |
| x |
(2)当0<x<1时,y1<y2;
当x=1时,y1=y2;
当x>1时,y1>y2;
(3)当1≤x≤2时y2的取值范围为
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
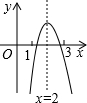 已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )| A、abc<0 |
| B、-3a+c<0 |
| C、b2-4ac≥0 |
| D、将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c |
已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
| A、a是无理数 | |||||
| B、a是方程x2-8=0的一个解 | |||||
| C、a是8的算术平方根 | |||||
D、a满足不等式组
|
 如图,在△ABC中,∠C=90°,BC=1,AC=2,四边形CA1B1C1、A1A2B2C2、A2A3B3C3…都是正方形,且A1、A2、A3…在AC边上,B1、B2、B3…在AB边上.则线段BnCn的长用含n的代数式表示为
如图,在△ABC中,∠C=90°,BC=1,AC=2,四边形CA1B1C1、A1A2B2C2、A2A3B3C3…都是正方形,且A1、A2、A3…在AC边上,B1、B2、B3…在AB边上.则线段BnCn的长用含n的代数式表示为 某冷饮店一天售出各种口味雪糕数量的扇形统计图如图,其中售出红豆口味的雪糕200支,那么售出水果口味雪糕的数量是
某冷饮店一天售出各种口味雪糕数量的扇形统计图如图,其中售出红豆口味的雪糕200支,那么售出水果口味雪糕的数量是 如图,已知E、F分别为?ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:EF与MN互相平分.
如图,已知E、F分别为?ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:EF与MN互相平分.