题目内容
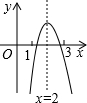 已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )| A、abc<0 |
| B、-3a+c<0 |
| C、b2-4ac≥0 |
| D、将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c |
考点:二次函数图象与系数的关系,二次函数图象与几何变换
专题:数形结合
分析:A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0.
B.根据图知对称轴为直线x=2,即-
=2,得b=-4a,再根据图象知当x=1时,y<0,即可判断;
C.由抛物线与x轴有两个交点,可得b2-4ac>0;
D.把二次函数y=ax2+bx+c化为顶点式,再求出平移后的解析式即可判断.
B.根据图知对称轴为直线x=2,即-
| b |
| 2a |
C.由抛物线与x轴有两个交点,可得b2-4ac>0;
D.把二次函数y=ax2+bx+c化为顶点式,再求出平移后的解析式即可判断.
解答:解:A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;
B.根据图知对称轴为直线x=2,即-
=2,得b=-4a,再根据图象知当x=1时,y=a+b+c=a-4a+c=-3a+c<0,故本选项正确;
C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;
D.y=ax2+bx+c=a(x+
)2+
,
∵-
=2,
∴原式=a(x-2)2+
,
∴向左平移2个单位后所得到抛物线的解析式为y=ax2+
,故本选项错误;
故选:B.
B.根据图知对称轴为直线x=2,即-
| b |
| 2a |
C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;
D.y=ax2+bx+c=a(x+
| b |
| 2a |
| 4ac-b2 |
| 4a |
∵-
| b |
| 2a |
∴原式=a(x-2)2+
| 4ac-b2 |
| 4a |
∴向左平移2个单位后所得到抛物线的解析式为y=ax2+
| 4ac-b2 |
| 4a |
故选:B.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点和抛物线与x轴交点的个数确定.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.
其中说法正确的有( )
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.
其中说法正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
下列几何体的主视图、俯视图和左视图都是长方形的是( )
A、 |
B、 |
C、 |
D、 |
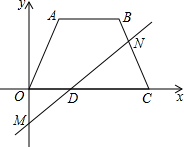 如图,在平面直角坐标系中,梯形OABC各顶点的坐标分别为O(0,0),A(2,3),B(4,3),C(6,0).点M的坐标为(0,-1),D是线段OC上的一个动点,当D点从O点向C点移动时,直线MD与梯形的一边交于点N.设点D的横坐标为t.
如图,在平面直角坐标系中,梯形OABC各顶点的坐标分别为O(0,0),A(2,3),B(4,3),C(6,0).点M的坐标为(0,-1),D是线段OC上的一个动点,当D点从O点向C点移动时,直线MD与梯形的一边交于点N.设点D的横坐标为t. 如图,一次函数y1=x+1的图象与反比例函数
如图,一次函数y1=x+1的图象与反比例函数