题目内容
 如图,在△ABC中,∠C=90°,BC=1,AC=2,四边形CA1B1C1、A1A2B2C2、A2A3B3C3…都是正方形,且A1、A2、A3…在AC边上,B1、B2、B3…在AB边上.则线段BnCn的长用含n的代数式表示为
如图,在△ABC中,∠C=90°,BC=1,AC=2,四边形CA1B1C1、A1A2B2C2、A2A3B3C3…都是正方形,且A1、A2、A3…在AC边上,B1、B2、B3…在AB边上.则线段BnCn的长用含n的代数式表示为考点:相似三角形的判定与性质,正方形的性质
专题:规律型
分析:根据题意得出△BB1C1∽△BAC,进而求出B1C1=
,同理可得出:B2C2=(
)2,B3C3=(
)3…进而得出答案.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:由题意可得:B1C1∥AC,
∴△BB1C1∽△BAC,
∴
=
,
∵CC1=B1C1,
∴
=
,
解得:B1C1=
,
故A1B1=
,AA1=
,
同理可得出:B2C2=(
)2,B3C3=(
)3…
∴线段BnCn的长用含n的代数式表示为:(
)n.
故答案为:(
)n.
∴△BB1C1∽△BAC,
∴
| BC1 |
| BC |
| B1C1 |
| AC |
∵CC1=B1C1,
∴
| B1C1 |
| 2 |
| 1-C1B1 |
| 1 |
解得:B1C1=
| 2 |
| 3 |
故A1B1=
| 2 |
| 3 |
| 4 |
| 3 |
同理可得出:B2C2=(
| 2 |
| 3 |
| 2 |
| 3 |
∴线段BnCn的长用含n的代数式表示为:(
| 2 |
| 3 |
故答案为:(
| 2 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质,得出线段BnCn长的变化规律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
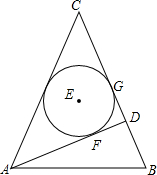 如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE. 如图,一次函数y1=x+1的图象与反比例函数
如图,一次函数y1=x+1的图象与反比例函数