题目内容
20．一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，然后放回，再随机摸出一个小球，两次摸出的小球标号的和为5的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{2}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的小球标号和5为的情况，再利用概率公式即可求得答案．
解答 解：根据题意，画树状图如下：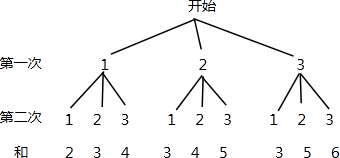
共有9种等可能结果，其中两次摸出的小球标号的和为5的有2种，
∴两次摸出的小球标号的和为5的概率是$\frac{2}{9}$，
故选：B．
点评 此题考查了树状图法与列表法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
如图，在?ABCD中，BD是对角线，且DB⊥BC，E、F分别为边AB、CD的中点．求证：四边形DEBF是菱形．
11．某公司全体员工年薪的具体情况如表：
则该公司全体员工年薪制的中位数比众数多0.5万元．
| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 | 3 |
| 员工数/人 | 1 | 2 | 3 | 4 | 5 | 6 | 4 |
15．某射击队要从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
小明根据统计结果计算了甲的平均数和方差，方法如下：
$\overline{{x}_{甲}}$=$\frac{1}{6}$（10+8+9+8+10+9）=9（环）
s2=$\frac{1}{6}$[（10-9）2+（8-9）2+（9-9）2+（8-9）2+（10-9）2+（9-9）2]=$\frac{2}{3}$
请根据以上信息，解答下列问题：
（1）请参考小明的方法分别计算乙的平均数和方差；
（2）请根据调查结果，从平均数和方差的角度分析选谁去参加比赛较为合适？
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$（10+8+9+8+10+9）=9（环）
s2=$\frac{1}{6}$[（10-9）2+（8-9）2+（9-9）2+（8-9）2+（10-9）2+（9-9）2]=$\frac{2}{3}$
请根据以上信息，解答下列问题：
（1）请参考小明的方法分别计算乙的平均数和方差；
（2）请根据调查结果，从平均数和方差的角度分析选谁去参加比赛较为合适？
如图，矩形ABCD中，AB=5，AD=8，E是AD上一动点，把△ABC沿BE折叠，当点A的对应点A′落在矩形ABCD的对称轴上时，则AE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$．
如图，一次函数y=kx+b分别与x轴、y轴交于A，B两点，与反比例函数y=-$\frac{4}{x}$交于点C，B为AC的中点，则△AOC的面积为2．