题目内容
15.某射击队要从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
分析 (1)根据小明计算平均数与方差的方法列出算式进行计算即可得出乙的平均数和方差;
(2)根据方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定解答即可.
解答 解:(1)$\overline{{x}_{乙}}$=$\frac{1}{6}$(10+7+10+10+9+8)=9(环),
s2=$\frac{1}{6}$[(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2]=$\frac{4}{3}$;
(2)选甲去参加比赛较为合适.理由如下:
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,甲的方差<乙的方差,
∴甲的成绩比较稳定,
∴选甲去参加比赛更合适.
点评 本题考查的是平均数、方差的计算和性质,掌握平均数、方差的计算公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 某几何体的三视图如图所示,则其侧面积是( )
某几何体的三视图如图所示,则其侧面积是( )
 某几何体的三视图如图所示,则其侧面积是( )
某几何体的三视图如图所示,则其侧面积是( )| A. | 12π | B. | 6π | C. | 4π | D. | 6 |
20.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,然后放回,再随机摸出一个小球,两次摸出的小球标号的和为5的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
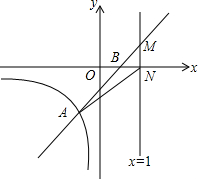 直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0)
直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0) 如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D. 如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E.
如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E. 如图,在以BC为直径的半圆O中,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
如图,在以BC为直径的半圆O中,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.