题目内容
12.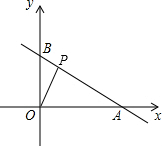 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).(1)求k的值;
(2)若点P(x,y)是直线在第一象限内的动点(0<x<8),试确定点P的坐标,使△OAP的面积为12.
分析 (1)直接把A的坐标(8,0)代入y=kx+6就可以求出k的值;
(2)根据三角形的面积公式S△OPA=$\frac{1}{2}$OA•y,然后把y转换成x,△OPA的面积S与x的函数关系式就可以求出了,再把S=12代入的解析式里.就可以求出x,然后确定P的坐标.
解答 解:(1)把点A(8,0)代入y=kx+6,
得8k+6=0,解得k=-$\frac{3}{4}$;
(2)∵点P(x,y)在第一象限内的直线y=-$\frac{3}{4}$x+6上,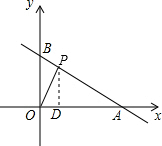
∴点P的坐标为(x,-$\frac{3}{4}$x+6)且x>0,-$\frac{3}{4}$x+6>0
过点P作PD⊥x轴于点D,则△OPA的面积=$\frac{1}{2}$OA×PD
即S=$\frac{1}{2}$×8×(-$\frac{3}{4}$x+6),
∴S=-3x+24=12,
解得x=4,
把x=4代入y=-$\frac{3}{4}$x+6,得y=3,
这时,P有坐标为(4,3);
即当P运动到点(4,3)这个位置时,△OPA的面积为12.
点评 本题考查了待定系数法求函数的解析式,一次函数的图象的性质,还有三角形的面积公式,把求三角形的面积和一次函数的图象结合起来,综合性比较强.

练习册系列答案
相关题目
7.在Rt△ABC中,AB=3,AC=4,则BC的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
1.下列二次根式为最简二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{44}$ |
2.某工厂的大门是抛物线型水泥建筑物,大门地面宽为8m,两侧距地面3m处各有一个壁灯,两壁灯之间的水平距离为6m,则大门的高约为( )
| A. | 6.9m | B. | 7.0m | C. | 7.1m | D. | 6.8m |
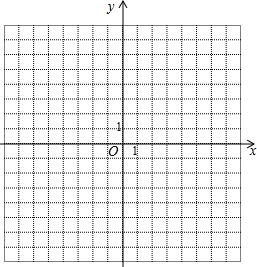 如图,在平面直角坐标系中,某四边形的四个顶点的坐标分别为:A(4,-2),B(6,2),C(4,6),D(2,2).
如图,在平面直角坐标系中,某四边形的四个顶点的坐标分别为:A(4,-2),B(6,2),C(4,6),D(2,2).
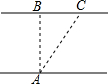 某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).
某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).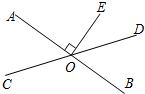 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为55°°.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为55°°.