题目内容
20.某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
分析 (1)根据折线统计图得出A,B两种品牌冰箱的销售台数,分别求出中位数与方差即可;
(2)根据(1)的结果比较即可得到结果.
解答 解:(1)A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,B品牌冰箱月销售量的中位数为15台,
∵$\overline{{x}_{A}}$=$\frac{13+14+15+16+17}{5}$=15(台);$\overline{{x}_{B}}$=$\frac{10+14+15+16+20}{5}$=15(台),
则SA2=$\frac{(13-15)^{2}+(14-15)^{2}+(15-15)^{2}+(16-15)^{2}+(17-15)^{2}}{5}$=2,SB2=$\frac{(10-15)^{2}+(14-15)^{2}+(15-15)^{2}+(16-15)^{2}+(20-15)^{2}}{5}$=10.4;
(2)∵SA2<SB2,
∴A品牌冰箱的月销售量稳定.
点评 此题考查了折线统计图,中位数,以及方差,熟练掌握各自的求法是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
10. 如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
 如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )| A. |  | B. |  | C. |  | D. |  |
15.在课外活动时间,小王、小丽、小华做“互相踢毽子”游戏,毽子从一人传到另一人就记为踢一次.若从小丽开始,经过两次踢毽后,毽子踢到小华处的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
9. 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
青年人日均发微信条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):青年人日均发微信条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<10) | 90 | 0.3 |
| B级(10≤m<20) | 120 | a |
| C级(20≤m<30) | b | 0.2 |
| D级(30≤m<40) | 30 | 0.1 |
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
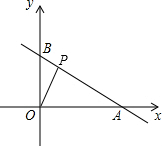 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).