题目内容
17.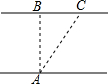 某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).
某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).
分析 根据题意得出∠ABC=90°,由勾股定理求出AB即可.
解答 解:根据题意得:∠ABC=90°,
则AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{51{0}^{2}-24{0}^{2}}$=450(米),
即该河的宽度为450米.
点评 本题考查了勾股定理的运用;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2. 如图,直线AB,CD相交于点O,∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )
如图,直线AB,CD相交于点O,∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )
 如图,直线AB,CD相交于点O,∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )
如图,直线AB,CD相交于点O,∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )| A. | 165° | B. | 155° | C. | 150° | D. | 130° |
9. 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
青年人日均发微信条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):青年人日均发微信条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<10) | 90 | 0.3 |
| B级(10≤m<20) | 120 | a |
| C级(20≤m<30) | b | 0.2 |
| D级(30≤m<40) | 30 | 0.1 |
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
6.在某中学举行的演讲比赛中,七年级5名参赛选手的成绩及平均成绩如下表所示:
那么根据表中提供的数据,计算这5名选手比赛成绩的方差是6.8.
| 选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 平均成绩 |
| 得分 | 90 | 95 | 93 | 89 | 88 | 91 |
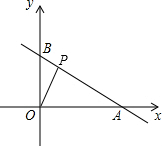 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).