题目内容
7.已知2+$\sqrt{3}$是方程x2-5sinθ•x+1=0的一个根,求sinθ.分析 根据方程的解满足方程,可得关于θ的锐角三角函数,根据特殊角三角函数值,可得答案.
解答 解:由2+$\sqrt{3}$是方程x2-5sinθ•x+1=0的一个根,得
4+4$\sqrt{3}$+3-(10+5$\sqrt{3}$)sinθ+1=0.
化简,得
(10+5$\sqrt{3}$)sinθ=8+4$\sqrt{3}$,
sinθ=$\frac{8+4\sqrt{3}}{10+5\sqrt{3}}$=$\frac{(8+4\sqrt{3})(10-5\sqrt{3})}{25}$=$\frac{4}{5}$.
点评 本题考查了解一元二次方程,把方程的解代入方程得出关于sinθ的方程是解题关键,注意要分母有理化.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
17.若$\sqrt{\frac{x-2}{3-x}}$=$\frac{\sqrt{x-2}}{\sqrt{3-x}}$成立,则x的取值范围为( )
| A. | x≥2 | B. | x≤3 | C. | 2≤x≤3 | D. | 2≤x<3 |
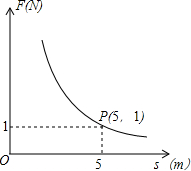 在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m.
在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m. 将图中△ABC,以点G为位似中心,缩小为原来的0.5倍,得到△A′B′C′,写出变化前后两个三角形各顶点的坐标.
将图中△ABC,以点G为位似中心,缩小为原来的0.5倍,得到△A′B′C′,写出变化前后两个三角形各顶点的坐标. 如图,用(0,0)表示点O的位置,用(3,2)表示点M的位置,则点N的位置可表示为(6,3).
如图,用(0,0)表示点O的位置,用(3,2)表示点M的位置,则点N的位置可表示为(6,3).