题目内容
7. 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2-2x-3,AC为半圆的直径.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2-2x-3,AC为半圆的直径.(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
分析 (1)连接DE,根据坐标轴上点的坐标特征求出A、B、C的坐标,根据题意求出半圆的直径,根据勾股定理求出OD的长,得到点D的坐标;
(2)根据射影定理求出EF的长,得到点F的坐标,运用待定系数法求出经过点D的果圆的切线DF的解析式;
(3)根据切线的性质得到经过点B的果圆的切线与抛物线只有一个公共点,根据一元二次方程的判别式解答即可求出点M的坐标,根据三角形的面积公式计算即可.
解答 解: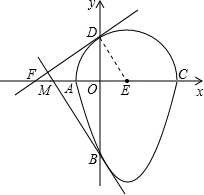 (1)连接DE,
(1)连接DE,
∵y=x2-2x-3,
∴x=0时,y=-3,
y=0时,x1=-1,x2=3,
∴点A的坐标为(-1,0),点B的坐标为(0,-3),点C的坐标为(3,0),
∵AC=4,
∴AE=DE=2,
∴OE=1,
∴OD=$\sqrt{D{E}^{2}-O{E}^{2}}$=$\sqrt{3}$,
∴D点的坐标为(0,$\sqrt{3}$);
(2)∵DF是果圆的切线,
∴ED⊥DF,又DO⊥EF,
∴DE2=EO•EF,
∴EF=4,则OF=3,
∴点F的坐标为(-3,0),
设经过点D的果圆的切线DF的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-3k+b=0}\\{b=\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\sqrt{3}}\end{array}\right.$.
∴经过点D的果圆的切线DF的解析式为y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$;
(3)设经过点B的果圆的切线的解析式为:y=ax+c,
∵点B的坐标为(0,-3),
∴经过点B的果圆的切线的解析式为:y=ax-3,
由题意得,方程组$\left\{\begin{array}{l}{y=ax-3}\\{y={x}^{2}-2x-3}\end{array}\right.$只有一个解,
即一元二次方程x2-(a+2)x=0有两个相等的实数根,
△=(a+2)2-4×1×0=0,
解得a=-2,
∴经过点B的果圆的切线的解析式为:y=-2x-3,
当y=0时,x=-$\frac{3}{2}$,
∴点M的坐标为(-$\frac{3}{2}$,0),即OM=$\frac{3}{2}$,
∴△OBM的面积=$\frac{1}{2}$×OM×OB=$\frac{9}{4}$.
点评 本题考查的是圆的切线的性质、待定系数法求一次函数的解析式、一元二次方程根与系数的关系以及坐标与图形的性质,灵活运用相关的定理、数形结合思想以及方程思想是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 3tan50° | B. | 3sin50° | C. | 3tan40° | D. | 3sin40° |
| 价格/类型 | A型 | B型 |
| 进价(元/副) | 60 | 140 |
| 标价(元/副) | 100 | 200 |
(2)若A型球拍按标价的9折出售,B型球拍按标价的8折出售,那么这批球拍全部售出后,超市共可获利多少元?
| A. | 图象必经过点(-1,2) | B. | 当x>0时,y随x的增大而增大 | ||
| C. | 若x>1,则y<-2 | D. | 图象在第二、四象限内 |
| A. | 7个 | B. | 5个 | C. | 4个 | D. | 无数个 |
| A. | -|-2|<-3 | B. | 绝对值小于4的正数有-4,-3,-2,-1 | ||
| C. | (-2)n<0(n为正整数) | D. | 若a2=(-2)2,则a=±2 |
 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是x=2,与x轴的一个交点是(-1,0),有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是x=2,与x轴的一个交点是(-1,0),有下列结论:
 已知:如图,平面直角坐标系中,A(0,8),B(0,4),点C是x轴上一点,点D为OC的中点.
已知:如图,平面直角坐标系中,A(0,8),B(0,4),点C是x轴上一点,点D为OC的中点.