题目内容
16.如图,在Rt△ABC中,∠ACB=90°,点O是边AC上一点,以OA为半径作圆O与边AB相交于点D.
(1)如图1,当圆O过点C时,取BC边中点E,连接DE,求证:DE是圆O的切线;
(2)如图2,圆O与边AC相交于点F,若AO=OF=FC,AD=BD,求∠BAC的正切值;
(3)如图3,若$\frac{AD}{DB}$=$\frac{4}{5}$,AC=$\sqrt{2}$AD,求$\frac{AO}{OC}$的值.
分析 (1)首先证明ED=EC,推出∠EDC=∠ECD,由OD=OC,推出∠OCD=∠ODC,由∠OCD+∠ECD=90°,推出∠ODC+∠EDC=90°即可解决问题;
(2)如图2中,连接DF、BF.只要证明DF垂直平分线段AB,可得BF=AF=2OF,推出∠CFB=60°即可解决问题;
(3)如图3中,延长GC交⊙O于F,连接DF、OG.由OC⊥FG,推出CF=CG,设CF=CG=x,BG=y,AD=4k,BD=5k,AC=4$\sqrt{2}$k,构建方程组,求出x、y即可,再在Rt△
OCG中,设OA=OG=m,利用勾股定理列出方程即可解决问题;
解答 解:(1)如图1中,连接OD、CD.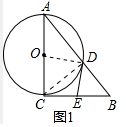
∵AC是直径,
∴∠ADC=∠CDB=90°,
∵CE=EB,
∴DE=EC=EB,
∴∠EDC=∠ECD,
∵OC=OD,
∴∠OC=∠ODC,
∵∠OCD+∠DCB=∠ACB=90°,
∴∠ODC+∠EDC=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)如图2中,连接DF、BF.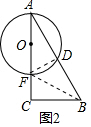
∵AF是直径,
∴∠ADF=90°,
∴FD⊥AB,
∵AD=BD,
∴FA=FB,
∵OA=OF=FC,
∴BF=2FC,
在Rt△BCF中,cos∠CFB=$\frac{CF}{BF}$=$\frac{1}{2}$,
∴∠CFB=60°,
∵FA=FB,
∴∠FAB=∠FBA,
∵∠CFB=∠FAB+∠FBA=60°,
∴∠FAB=∠FBA=30°,
∴tan∠BAC=tan30°=$\frac{\sqrt{3}}{3}$.
(3)如图3中,延长GC交⊙O于F,连接DF、OG.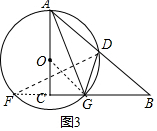
∵OC⊥FG,
∴CF=CG,设CF=CG=x,BG=y,AD=4k,BD=5k,AC=4$\sqrt{2}$k,
在Rt△ACB中,∵AC2+BC2=AB2,
∴32k2+(x+y)2=81k2 ①,
由△BDF∽△BGA,可得BD•BA=BG•BF,
∴45k2=y(y+2x) ②
由①②可得:x=2k,y=5k,设OA=OG=m,
在Rt△OCG中,∵OG2=OC2+CG2,
∴m2=(4$\sqrt{2}$k-m)2+(2k)2,
∴m=$\frac{9\sqrt{2}}{4}$k,
∴OA=$\frac{9\sqrt{2}}{4}$k,OC=$\frac{7\sqrt{2}}{4}$k,
∴$\frac{OA}{OC}$=$\frac{\frac{9\sqrt{2}}{4}k}{\frac{7\sqrt{2}}{4}k}$=$\frac{9}{7}$.
点评 本题考查圆综合题、切线的判定、勾股定理、相似三角形的判定和性质、二元二次方程组等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数构建方程组解决问题,属于中考常考题型.

| A. | x2=3x | B. | (x-2)2=3x-6 | C. | 4x2+4x+1=0 | D. | (x+2)(2x-1)=5 |
 如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.
如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.

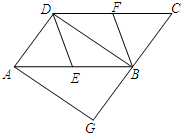 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.