题目内容
6. 如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.
如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.(1)求证:AE=CF;
(2)连接DE,若AD=24,AB=15,DE 平分∠ADC,求BE的长度.
分析 (1)根据平行四边形的性质可证明△ABE≌△CDF,则可求得AE=CF;
(2)由平行四边形的性质结合角平分线的定义可求得∠EDC=∠CED,则可求得CE的长,进一步可求得BE的长.
解答 (1)证明:
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠B=∠CDF,
在△ABE和△CDF中
$\left\{\begin{array}{l}{∠BAE=∠CDF}\\{AB=CD}\\{∠B=∠CDF}\end{array}\right.$
∴△ABE≌△CDF(ASA),
∴AE=CF;
(2)解:
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠CED,
∴CD=CE=15,
∵BC=AD=24,
∴BE=BC-CE=24-15=9.
点评 本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键.

练习册系列答案
相关题目
17.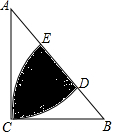 如图,在△ABC中,∠ACB=90°,AC=BC=4,分别以点A,B为圆心,AC,BC的长为半径作圆,分别交AB于点D,E,则弧DE,弧CE和线段DE围成的封闭图形(图阴影部分)的面积为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,分别以点A,B为圆心,AC,BC的长为半径作圆,分别交AB于点D,E,则弧DE,弧CE和线段DE围成的封闭图形(图阴影部分)的面积为( )
 如图,在△ABC中,∠ACB=90°,AC=BC=4,分别以点A,B为圆心,AC,BC的长为半径作圆,分别交AB于点D,E,则弧DE,弧CE和线段DE围成的封闭图形(图阴影部分)的面积为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,分别以点A,B为圆心,AC,BC的长为半径作圆,分别交AB于点D,E,则弧DE,弧CE和线段DE围成的封闭图形(图阴影部分)的面积为( )| A. | 4π-8 | B. | 6π-8 | C. | 8π-8 | D. | 10π-8 |
14.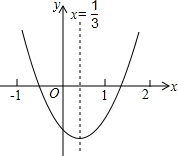 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1. 如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
 如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4000米到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )| A. | 2000米 | B. | 3000米 | C. | 4000米 | D. | 5000米 |
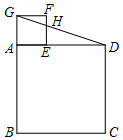 如图,在正方形ABCD和正方形AEFG中,顶点E在边AD上,连接DG交EF于点H,若FH=1,EH=2,则DG的长为$3\sqrt{10}$.
如图,在正方形ABCD和正方形AEFG中,顶点E在边AD上,连接DG交EF于点H,若FH=1,EH=2,则DG的长为$3\sqrt{10}$.
 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).