题目内容
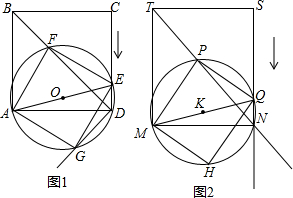
2.如图1,在正方形ABCD中,点E从点C出发,沿CD向点D运动,连结AE,以AE为直径作⊙O,交正方形的对角线BD于点F,连结AF,EF,以点D为垂足,作BD的垂线,交⊙O于点G,连结GA,GE.[发现]
(1 )在点E运动过程中,找段AF=EF(填“>”、“=”或“<”)
(2)求证:四边形AGEF是正方形;
[探究](3)当点E在线段CD上运动时,探索BF、FD、AE之间满足的等量关系,开加以证明;当点E在线段CD的延长线上运动时,上述等量关系是否成立?(答“成立”或“不成立”)
[拓展]
(4)如图2,矩形MNST中,MN=6,MT=8,点Q从点S出发,沿射线SN运动,连结MQ,以MQ为直径作⊙K,交射线TN于点P,以MP,QP为邻边作⊙K的内接矩形MHQP.当⊙K与射线TN相切时,点Q停止运动,在点Q运动过程中,设矩形MHQP的面积为S,MP=m.
①求S关于m的函数关系式,并求S的最值;
②直接写出点H移动路线的长.
分析 (1)由四边形ABCD是正方形,得到∠ADB=∠AEF=45°,推出△AEF是等腰直角三角形,于是得到结论;
(2)根据圆周角定理得到FG为⊙O的直径,推出∠FAG=∠FEG=90°,根据正方形的判定定理即可得到结论;
(3)根据已知条件得到△BAF≌△DAG,证得BF=GD,根据勾股定理得到GD2+FD2=FG2,即可得到结论;
(4)①根据圆周角定理得到∠MQP=∠MNP,∠MPQ=∠TMN=90°,推出△MPQ∽△TMN,根据相似三角形的性质得到S=2S△MPQ=2•$\frac{3}{8}$m2=$\frac{3}{4}$m2,当点Q在射线SN上运动过程中,点P在TN上运动,当点P与点T重合时,MP取得最大值,即m大=MT=8;当MP⊥TN时,MP取得最小值,于是得到结论;
②如图3,因为当⊙K与射线TN相切时,点Q停止运动,于是得到点H的起点为点N,终点为图3中的点H,点H移动的路线即为线段NH,根据相似三角形的性质即可得到结论.
解答 解:(1)=;
理由:∵四边形ABCD是正方形,
∴∠ADB=∠AEF=45°,
∵AE是⊙O的直径,
∴∠AFE=90°,
∴△AEF是等腰直角三角形,
∴AE=EF,
故答案为:=;
(2)证明:如图1,连接FG,
∵∠FDG=90°,
∴FG为⊙O的直径,
∴∠FAG=∠FEG=90°,
又∵AE是⊙O的直径,
∴∠AFE=∠AGE=90°,
由(1)知AF=EF,
∴四边形AGEF是正方形;
(3)如图1,连接FG,
∵∠BAD=∠FAG=90°,
∴∠BAF=∠DAG,
在△BAF与△DAG中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠DAG}\\{AF=AG}\end{array}\right.$,
∴△BAF≌△DAG,
∴BF=GD,
又∵AE=FG,
∴在Rt△FDG中,GD2+FD2=FG2,
即BF2+FD2=AE2,
当点E在线段CD的延长线上运动时,上述等量关系仍然成立;
(4)①如图2,在以MQ为直径作⊙K中,
∵∠MQP=∠MNP,∠MPQ=∠TMN=90°,
∴△MPQ∽△TMN,S△TMN=$\frac{TM•MN}{2}$=$\frac{8×6}{2}$=24,
∴$\frac{{{S_{△MPQ}}}}{{{S_{△TMN}}}}={({\frac{MP}{TM}})^2}$,$\frac{{{S_{△MPQ}}}}{24}={({\frac{m}{8}})^2}$,${S_{△MPQ}}=\frac{3}{8}{m^2}$,
∴S=2S△MPQ=2•$\frac{3}{8}$m2=$\frac{3}{4}$m2,
当点Q在射线SN上运动过程中,点P在TN上运动,
当点P与点T重合时,MP取得最大值,即m大=MT=8;
当MP⊥TN时,MP取得最小值,即m小=$\frac{MT•MN}{TN}=\frac{8×6}{10}=\frac{24}{5}$,
∴$\frac{24}{5}$≤m≤8,由$S=\frac{3}{4}{m^2}$得,
当m=8时,${S_大}=\frac{3}{4}×{8^2}=48$;
当m=$\frac{24}{5}$时,${S_小}=\frac{3}{4}×{({\frac{24}{5}})^2}=\frac{432}{25}$;
②如图3,连接NH并延长,在点Q的运动过程中,
始终有∠MNH=∠MTN=定值,因为当⊙K与射线TN相切时,点Q停止运动,
∴点H的起点为点N,终点为图3中的点H,点H移动的路线即为线段NH,
∵△MHN∽△STN,
∴$\frac{HN}{TN}=\frac{MN}{SN}$,即$\frac{HN}{10}=\frac{6}{8}$,
∴HN=$\frac{15}{2}$,
∴点H移动的路线长为$\frac{15}{2}$.
点评 本题考查了正方形的性质和判定,矩形的性质,等腰直角三角形的性质,相似三角形的判定和性质,勾股定理,圆周角定理,全等三角形的判定和性质,正确的理解题意,画出图形是解题的关键.

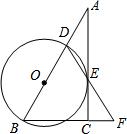 在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F,BD=BF.
在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F,BD=BF.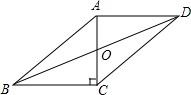 如图,在?ABCD中,AC⊥BC,且AD=8,AB=10,则△BOC的面积=12.
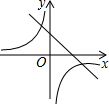
如图,在?ABCD中,AC⊥BC,且AD=8,AB=10,则△BOC的面积=12. 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )






 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )


