题目内容
7.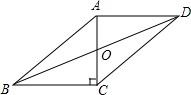 如图,在?ABCD中,AC⊥BC,且AD=8,AB=10,则△BOC的面积=12.
如图,在?ABCD中,AC⊥BC,且AD=8,AB=10,则△BOC的面积=12.
分析 直接利用平行四边形的性质结合勾股定理得出AC的长,再利用直角三角形面积求法得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=8,AO=CO,BO=DO,
∵AC⊥BC,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6,
∴CO=3,
∴△BOC的面积为:$\frac{1}{2}$×8×3=12.
故答案为:12.
点评 此题主要考查了平行四边形的性质以及勾股定理,正确得出AC的长是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
17.下列二次根式中,不能与$\sqrt{3}$合并的是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{27}$ |
12.下列四个数中,相反数是-$\frac{1}{5}$的数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
19.据大连市公安局统计,2016年全市约有410000人换二代居民身份证,将410000用科学记数法表示应为( )
| A. | 0.41×104 | B. | 41×104 | C. | 4.1×106 | D. | 4.1×105 |
 如图,已知菱形ABCD中,AC=6cm,BD=8cm,则菱形的高AE为$\frac{24}{5}$cm.
如图,已知菱形ABCD中,AC=6cm,BD=8cm,则菱形的高AE为$\frac{24}{5}$cm.
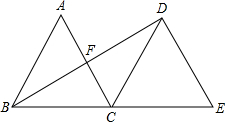 如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.
如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长是2$\sqrt{3}$.