题目内容
12. 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 点E在运动过程中,AE⊥EF是保持不变的,则可以证出△ABE∽△ECF,通过边的比值计算得出y与x的函数关系式为二次函数,从而确定了选项在C、D中产生,再通过配方法得出顶点坐标就能得到答案.
解答 解:∵AE⊥EF,∴∠AEB+∠FCE=90°
∵四边形ABCD是正方形,∴∠B=∠C=90° AB=BC=4,
∴∠BAE+∠AEB=90°,∴∠BAE=∠FCE,
∴△ABE∽△ECF,∴$\frac{AB}{EC}=\frac{BE}{FC}$,
∵BE=x,FC=y,∴EC=4-x,则有$\frac{4}{4-x}=\frac{x}{y}$,
整理后得 y=$-\frac{1}{4}$x2+x 配方后得到y=-$\frac{1}{4}$(x-2)2+1
从而得到图象为抛物线,开口朝下,顶点坐标为(2,1).
故选C.
点评 本题将正方形性质、相似三角形及二次函数图象巧妙的融合在一题中,计算量不大,但是涉及的知识点都很重要,是道考察学生综合运用知识的好题.

练习册系列答案
相关题目
1.据统计,2015年我国高新技术产品出口总额达40570亿元,将数据40570亿用科学记数法表示为( )
| A. | 4.0570×109 | B. | 0.40570×1010 | C. | 40.570×1011 | D. | 4.0570×1012 |
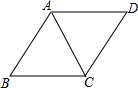 如图,菱形ABCD的边长为5cm,cosB=0.6,则对角线AC的长为2$\sqrt{5}$cm.
如图,菱形ABCD的边长为5cm,cosB=0.6,则对角线AC的长为2$\sqrt{5}$cm.
 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.