Question

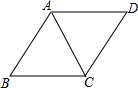
13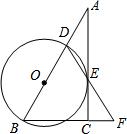．在△ABC中，∠ACB=90°，D是AB边上一点，以BD为直径的⊙O与边AC有公共点E，连结DE并延长，与BC的延长线交于点F，BD=BF．
（1）求证：AC是⊙O的切线；
（2）若BF=8，AD=4，求CF的长．

Answer 1

分析 （1）连接OE，求出∠ODE=∠F=∠DEO，推出OE∥BC，得出OE⊥AC，根据切线的判定推出即可；
（2）设CF=x，证△AEO∽△ACB，得出关于x的方程，求出x即可．

解答 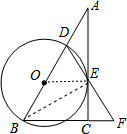（1）证明：连接BE，OE，
∵BD是直径，
∴BE⊥DF，
∵BD=BF，
∴DE=EF，
∴OE∥BF，
∵∠ACB=90°，
∵OE⊥AC，
∴AC是⊙O的切线；
（2）解：∵OE∥BC，
∴△AOE∽△ABC，
∴$\frac{AO}{AB}=\frac{OE}{BC}$，
设CF=x，则BC=8-x，则$\frac{8}{12}=\frac{4}{8-x}$，
解得x=2，
即CF=2．

点评 本题考查了等腰三角形的性质，切线的判定，平行线的性质和判定，相似三角形的性质和判定的应用，主要考查学生的推理和计算能力，用了方程思想．