题目内容
11．小伟在一次数学课外活动中发现一个奇特的现象：他随便说一个整数（不等于零），然后用这个整数去乘以比它大1的数，再减去这个数乘以比它小1的数的积，所得的差除以这个整数，最后结果总是2，你能说明其中的道理吗？分析 根据题意分别表示出关系式，进而利用整式混合运算法则化简求出答案．
解答 解：设这个整数为a，根据题意可得：
[a（a+1）-a（a-1）]÷a=2，
证明：∵[a（a+1）-a（a-1）]÷a
=（a2+a-a2+a）÷a
=2a÷a
=2，
∴[a（a+1）-a（a-1）]÷a=2．
点评 此题主要考查了整式的混合运算，正确掌握运算法则是解题关键．
练习册系列答案
相关题目
6．下列各式不是多项式x3-x的因式的是（ ）
| A． | x | B． | 3x-1 | C． | x-1 | D． | x+1 |
16．某商场为提高彩电销售人员的积极性，制定了新的工资分配方案．方案规定：每位销售人员的工资总额=基本工资+奖励工资．每位销售人员的月销售定额为10000元，在销售定额内，得基本工资200元；超过销售定额，超过部分的销售额按相应比例作为奖励工资．
（1）已知销售员甲本月分领到的工资总额为800元，请问甲本月的销售额为多少元？
（2）若销售员乙本月得到工资1300元，问乙本月的销售额为多少元？
（3）在（2）的条件下，已知乙本月销售A、B两种型号的彩电21台，且A型彩电的销售价为每台1000元，B型彩电的销售价为每台1500元，问乙本月销售A型彩电多少台？
（1）已知销售员甲本月分领到的工资总额为800元，请问甲本月的销售额为多少元？
（2）若销售员乙本月得到工资1300元，问乙本月的销售额为多少元？
（3）在（2）的条件下，已知乙本月销售A、B两种型号的彩电21台，且A型彩电的销售价为每台1000元，B型彩电的销售价为每台1500元，问乙本月销售A型彩电多少台？
| 销售额 | 奖励工资比例 |
| 超过0元但不超过5千元部分 | 5% |
| 超过0.5万元但不超过1万元部分 | 8% |
| 1万元以上的部分 | 10% |
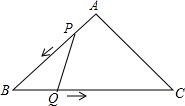已知：如图，△ABC是等腰直角三角形，∠A=90°，AB=AC=3cm，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，P的速度是1cm/s，Q的速度是$\sqrt{2}$cm/s．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s）．解答下列问题：